maturalne aniaa :): podstawa ostrosłupa jest prostokąt o bokach 1 i √2. Najkrótsza krawędz boczna jest prostopadła do podstawy , a najdłuzsza krawedz boczna jest nachylona do podstawy pod kątem 30 oblicz pole powierzchni całkowitej tego ostrosłupa.

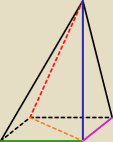
Patronus: Ok to niech zielona = 1, różowa = √2 niebieska jest ⊥do brązowej a brązowa i czerwona sa pod kątem 30 Ok to brązowa jest przekątna prostokata o bokach 1 i √2 to z Pitagorasa mozna obliczyć że ma √3

	√3		niebieska
tg kata między czerwoną a brązową to tg30 =		=
	3		√3

Zatem niebieska = 1 No to już dalej łatwo?

aniaa :): i to jest na pewno dobrze? bo mi zły wynik w polu wychodzi

Patronus: A jak dalej liczysz pole, na razie na pewno jest dobrze

aniaa :): własnie nie jestem pewna jak dalej i tak tylko próbowałam