trygonometria Tadzio: Mam w zadaniu naszkicować wykres funkcji f(x)= |sin x| / sin x, i podać rozwiązanie nierówności f(x)>0. Przede wszystkim jak to narysować? Drugi przykład to f(x)= tg x / |tg x| czy ktoś to rozumie byłbym wdzięczny bardzo

Artur z miasta Neptuna: jest to zadanie typu: narysuj:

	|x|
f(x) =
	x

jeżeli:

	x
x>0 to f(x) =		= 1
	x

	−x
jeżeli x<0 to f(x) =		= −1
	x

dla x=0 funkcja nie przyjmuje żadnej wartości (x=0 jest poza dziedziną funkcji) dotyczy to obu tych funkcji i każdej tego typu

Tadzio: tak a mógłbyś jeszcze dać podpowiedź jak to narysować? bo właśnie nie mogę się doszukać a wiem że kiedyś to miałem... ehhh skleroza nie boli

krystek: sinx≥0⇒f(x)=1 sinx<0 f(x)=−1 i teraz ustal dla jakich x spełnione są warunki nałożone na sinx.

Artur z miasta Neptuna: a dla sin(x) = 0 brak wartości

krystek: ok, sinx>0

Tadzio: wyszło mi to: 1. rozwiązałem to w przedziałach <0,π> 2. warunkiem było f(x)>0. wiec biorę pod uwagę wszystkie wart większe od 0 (za wyjątkiem 0) 3. wyszło mi to: x₁= ^π₂ 4. zapisuję to za pomoca wzoru x ∊ <^π₂ +2kπ> k∊C czy dobrze zrobiłem czy nadal nie czaję bazy...

Tadzio: oczywiście pkt 2 jest zbędny bo to nie jest nierówność tylko równanie... więc on odpada

Artur z miasta Neptuna: yyyyyyy co ... co oznacza <^π/₂ +2kπ> bo na pewno nie przedział domknięty po drugie .. dlaczego założenie w 1. skąd Ci wyszło 3.

Artur z miasta Neptuna: zacznijmy od tego ... co Ty obliczyłeś ?

Artur z miasta Neptuna: kiedy sin x > 0 czy kiedy sin x = 0

Tadzio: . 2. polecenie to było takie: naszkicować wykres funkcji f(x)= |sin x| / sin x, i podać rozwiązanie nierówności . f(x)>0 3. sin x = 1 bo narysowaniu wykresu przecina punkty ^π₂ itd.. dlatego tak zapisałem w 3.. a rozwiazywałem to w przedziale <0,π> 4. w 4 pkt to wynik...

Tadzio: moment... zaraz dam odp.. bo coś widze namieszałem.

Tadzio: <π/2 +2kπ> k∊C oznacza.. że ten punkt przecięcia będzie powtarzał się co K , litera k nalezy do liczb całkowitych więc podstawiając pod nią obojętnie jaką liczbe całkowitą otrzymamy punkt przeciecia się z sinx=1 a obliczałem w sin x > 0

Tadzio: <π/2 +2kπ> k∊C oznacza.. że ten punkt przecięcia będzie powtarzał się co K , litera k nalezy do liczb całkowitych więc podstawiając pod nią obojętnie jaką liczbe całkowitą otrzymamy punkt przeciecia się z sinx=1 a obliczałem w sin x > 0

Tadzio: https://matematykaszkolna.pl/strona/1582.html

Tadzio: sory.. bez przedziału to... π/2 +2kπ k∊C

krystek: Dla jakich x sinx>0 popatrz uważnie na wykres i zapisz !

Tadzio: x∊(kπ, π + 2kπ) k∊C

Tadzio: to chyba raczej to z tego co pokazałes: krystek

krystek: i teraz kreśl

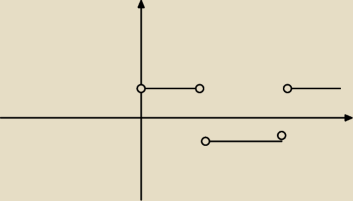
krystek: Wstaw odpowiednie wartości

krystek: I co rozumiesz?

Tadzio: tak już zrozumiałem.. wielkie dzięki serdecznie! jejku jak ta matme się szybko zapomina...