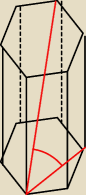
problem z obliczeniem objętości graniastosłupa prawidłowego sześciokątnego mario2020: zad. Oblicz objętość graniastosłupa prawidłowego sześciokątnego wiedząc że jego przekątna ma długość 9 cm a kąt zawarty pomiędzy nią a krótszą przekątną podstawy ma miarę 60 stopni. Jeżeli ktoś wiedziałby jak mam ugryźć to zadanie to będę wdzięczny

rumpek: Robiłem koledze przed chwilą rysunek właśnie odnośnie takiego graniastosłupa prawidłowego sześciokątnego: http://images43.fotosik.pl/1400/f3332930dc6074f0.jpg Rozwiązanie: Kąt który mamy podany w zadaniu to kąt α na moim rysunku. Liczymy teraz długość przekątnej podstawy:

	a√3
cos60o =
	9

1
	* 9 = a√3
2

	9
a√3 =		/ * √3
	2

	9√3
3a =		/ : 3
	2

	3√3
a =
	2

	a2√3
Aby obliczyć pole podstawy wystarczy podstawić wyliczone a pod wzór: Pp = 6 *
	4

Pozostało wyliczyć wysokość, również z związków trygonometrycznych:

	H
sin60o =
	9

√3		H
	=
2		9

	9√3
H =
	2

potem tylko: V = P_p * H koniec

mario2020: wielkie dzięki z kolejnymi zadaniami już sobie poradzę

mario2020: Tak teraz sobie pomyślałem trochę nad tym zadaniem i tutaj kąt α (w rozwiązaniu) to kąt zawarty pomiędzy KRÓTSZĄ przekątną graniastosłupa a KRÓTSZĄ przekątną podstawy tego graniastosłupa, a ja mam w zadaniu że jest to kąt który zawiera się pomiędzy DŁUŻSZĄ przekątną graniastosłupa a KRÓTSZĄ przekątną jego podstawy... Ale wyliczenia mi pasują w 100% do momentu kiedy liczymy H! ponieważ w tym przypadku to co kolega oznaczył H u mnie będzie przekątną prostokąta tworzącego ścianę boczną... niech ktoś powie że się mylę

mario2020: że nikt mi nie pomoże rozwiać moich wątpliwości?

kassia: halo halo

mario2020: wracając do zadania...

	81√3
Pp=		cm2
	8

i teraz mogę wyliczy d_b (przekątną bocznej ściany): czyli będzie to to samo wyliczenie co u kolegi tj. :

	db
sin60o=
	9

wynik będzie identyczny:

	9√3
db=
	2

mając teraz krawędź podstawy równa a i przekątna ściany bocznej możemy wyliczyć H a²=b²=c² u nas będzie wyglądać a²+H²=d_b² czyli: H²=d_b²−a²

	9√3
H2=(		)2−(3√32)2
	2

H²=54 H=√54 H=3√6 V=P_p*H

	81√3
v=		*3√6
	8

no i teraz najważniejsze czy jest to dobrze zrobione

mario2020: czyli że nikt mi nie pomoże?