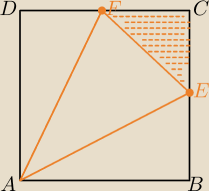
pigor: ... otóż, narysuj sobie kwadrat ABCD o boku długości 7cm i połącz np. środek E boku BC z
środkiem F boku CD oraz E z wierzchołkiem A i F z A. otrzymasz 4 trójkąty , z których
najmniejszy (o najkrótszych bokach) CEF ma pole
SCEF=12|CE|*|CF|=
12*3,5
2=
6,125cm2 − szukane pole trójkąta
ten trójkąt CEF jest po zagięciu wzdłuż linii AE, AF i EF podstawą ostrosłupa EFCA o
podstawie trójkąta prostokątnego równoramiennego CEF i wysokości AC⊥CF i AC⊥CE długości
|AC|=7 (wierzchołki BCD w tym ostrosłupie pokrywają się) , a ściany ABE i ADF są ⊥ do podstawy
CEF . ...


 H=AD=AB=7
H=AD=AB=7