funkcja homograficzna Ann: Rozwiąż równanie w zależności od parametru m:

	|x+2|
		= m+3
	|x−2|

stanęłam na y= ⁴_x −>[2,1] i co dalej? jaki rysunek ?

Ann: hm?

Eta:

	4
f(x)= |1+		|
	x−2

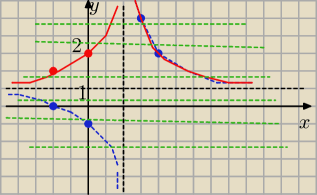
g(x)= m+3 brak rozwiązań dla m+3≤1 ⇒ dla m ≤ −2 dwa rozwiązania dla m+3 >1 ⇒ dla m > −2

rumpek:

|x + 2|		x + 2		4
	= |		| = |		+ 1|
|x − 2|		x − 2		x − 2

	x + 2		(x − 2) + 4		4		4
g(x) =		=		=		+ 1 ⇒ f(x) =		T = [2,1]
	x − 2		x − 2		x − 2		x

Wystarczy teraz narysować ten wykres co podałaś / podałeś, a następnie przenieść to co jest pod osią Ox nad nią. (pamiętając, że x≠2). Potem tylko odczytujesz rozwiązanie w zależności od parametru m, czyli: 0 rozwiązań dla m∊ .. 1 rozwiązanie dla ... itp.

rumpek: jak zwykle szybka i niezawodna Eta

Eta:

Eta: Jaka szybka? .......... widzisz ile musiałam się orysować

rumpek: Eto, ale wykres chyba źle odbity ?

Ann: hmm w notatkach od koleżanki z lekcji jest: m∊ {−3,−2} 1rozw wiec skad to sie wzielo?

Eta: Ajjjjjjjjjjjjj faktycznie ( ślepota

rumpek: tyle rysowania

Ann: właśnie nie odbijamy względem osi normalnej, a nie tej z przesuniecia[2,−3]?

rumpek: właśnie odbijamy względem tej osi normalnej (x≠2)

Ann: dziękuję

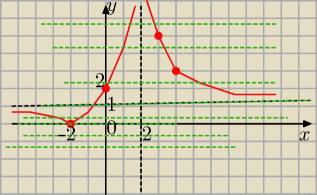
Eta: 0 rozwiązań dla m+3 <1 ⇒ dla m < −2 1 rozwiązanie dla m+3=0 i m+3=1 ⇒ dla m= −3 i m= −2 2 rozwiązania dla 0< m +3 <1 lub dla m+3 >1 m€ ......... dokończ sorry ......z poprzedni błędny wykres

Eta: