trapez OLa: Punkt E leży na ramieniu BC trapezu ABCD, w którym AB||CD. Udowodnij że |∡AED|=|∡BAE|+|∡CDE|.

pigor: .... przez punkt E poprowadź odcinek EF∥do podstaw trapezu (F∊ AD), wtedy sprawa prosta bo |∡AEF|=|∡BAE| i |∡DEF|=|∡CDE| ⇒ dodając stronami |∡AEF|+|∡DEF|=|∡BAE|+|∡CDE| ⇒ |∡AED|=|∡BAE|+|∡CDE| c.n.d. . ...

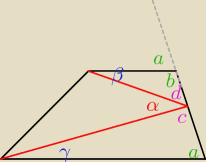
Artur z miasta Neptuna: wiesz, że a+b = 180^o (co pokazałem na rysunku ... przedłużając ramię trapezu) a także wiesz, że: c = 180 − a − γ oraz d = 180 − b − β oraz d+c+α = 180 więc: c+d = 180 + 180 − (a+b) − (β+γ) = 180 − (β+γ) oraz: d+c+α = 180 ⇔ α = 180 − (d+c) więc: α = 180 − (180 − (β+γ))) = 180 − 180 + (β+γ) = β+γ c.n.w.