Planimetria, matura rozszerzona Klekota: Na bokach AC i BC trójkąta ABC obrano punkty P i Q takie, że |AP| : |PC| = 2:1 oraz |BQ| : |QC| = 2:1. Odcinki AQ i BP i przecinają się w punkcie R . Wykaż, że pole czworokąta CPRQ jest równe polu trójkąta ARP. To zadanie z OKE Poznań − próbna matura, styczeń 2012.

Klekota: Widać, że trójkącik PQC ma 9 razy mniejsze pole niż ABC. Widać, że czworokąt ABQP jest trapezem. Z własności trapezu widać, że trójkąty ARP i BQR mają równe pola.... itd itd Ale jak dojść do równości pola ARP z polem CPRQ

Klekota: Hmmm... czy zadanie jest tak trudne, czy może tak trywialne, że nikt się nim nie interesuje?

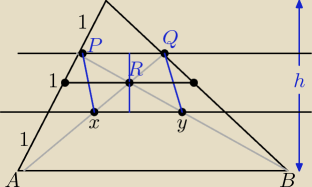
ejendi: mamy równoległobok XYPQ o wysokości h/3 Pole trapezu ABQP=Pt wysokość ΔPQR=h/6 PΔAQP=Pt−PΔABQ ciągnąć dalej, czy wystarczy?

Klekota: Bardzo dziękuję, pomogło mi skutecznie zwrócenie uwagi na to, że mogę wyznaczyć, jaką częścią dużego trójkąta jest każdy mały (każdy potrzebny). ARP i PRQC mają pola równe 1/6 ABC. Wcześniej próbowałam usilnie skorzystać z równości jakichś figur... nie szło za dobrze. A przecież wystarczyło policzyć. Jeszcze raz bardzo dziękuję!