planimetria zadanie: podstawy trapezu maja dlugosci a oraz b oblicz dlugosc odcinka rownoleglego do podstaw trapezu ktorego koncami sa punkty nalezace do amion trapezu jezeli wiesz ze dzieli on trapez na trapezy o rownych polach jakies podpowiedzi

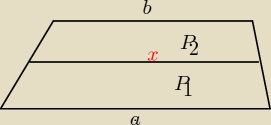
krystek: Wyjdź od P_t=P₁+P₂

zadanie: a+b/2*h=(a+x)/2*h₁+(x+b)/2*h₂ i co teraz h=h₁+h₂

zadanie:

Mila: Szkoda, że nie skończyłeś poprzedniej wersji. To będzie tak:

a+b		a+x		1		x+b		1
	*h =		*		h +		*		h / *2 /:h
2		2		2		2		2

	1		1
(a+b)=(a+x)*		+(b+x)*
	2		2

	1		1		1		1
a+b=		a+		x+		b+		x
	2		2		2		2

	a+b
x=
	2

zadanie: w odpowiedzi mam ze to jest √a²+b²/2 bo nie wiadomo czy ten odcinek jest rownooddalony od podstaw

Mila: Przepraszam moje rozwiązanie dotyczy poprzedniego Twojego zadania. Myślę, że to łatwiejszy sposób dla Ciebie. To zadanie trzeba rozwiązać, jak Krystek nie pomoże, to zrobię za kilka minut.

Mila:

1		1
	(a+x)h1=		(x+b)h2 pola równe
2		2

h=h₁ +h₂

	a+x		h2
(1)		=
	b+x		h1

z Twojego wzoru (a+x)h₁+(b+x)h₂=(a+b) (h₁+h₂) wymnożyc i pogrupowac wyrazy z h1 i h2 (a+x)h₁−(a+b)h₁=(a+b) h₂−(b+x)h₂ (x−b)h₁= (a−x)h₂

	x−b		h2
(2)		=
	a−x		h1

porównuje (1) i (2)

	a+x		x−b
		=		dokończ
	b+x		a−x

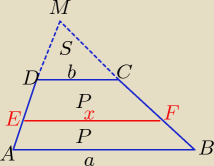
Eta: Można też tak: P, P, S zaznaczone pola , a,b,x −− podstawy trójkątów Mamy trzy trójkąty podobne Stosunek pól trójkątów podobnych równy jest kwadratowi skali podobieństwa zatem:

	S+P		x		2P+S		a
		= (		)2 i		= (		)2
	S		b		S		b

	P		x2		P		a2
(*) 1+		=		i (**) 2		+1=
	S		b2		S		b2

	P		x2
(*)		=		−1
	S		b2

	x2		a2
to: (**) 2*		−2+1=		/*b2
	b2		b2

	a2+b2
2x2 −b2=a2 ⇒ 2x2= a2+b2 ⇒ x2= √
	2

taki odcinek jest średnią kwadratową długości podstaw a i b trapezu

Eta:

	a2+b2
Poprawka : oczywiście x= √
	2