Wartość bezwzględna DużeK: Mam wrażenie że im więcej wiem, tym mam więcej wątpliwości. Równanie: | |x−1|−2|<1 założenie pierwsze |x−1|−2 > 0 <=> |x−1|>2 i dalej opuszczamy pierwszą wartośc bezwzględną: |x−1|−2<1 <=> |x−1|<3. Skoro założyliśmy że |x−1|>2 to wartość bezwzględna nie może równać się |x−1|<3. A jednak w rozwiązaniu nie wykluczają tego rozwiązania. Może ktoś to wyjaśnić

think: jak to nie może? po prostu wtedy 2 < |x − 1| < 3 przecież to co Ci wyszło się nie wyklucza gdyby było |x − 1| > 2 i |x − 1| < −3 to owszem nie byłoby rozwiązań

krystek: a może tak Ix−1I−2<1 i Ix−1I−2>−1 z interpr. geom i teraz Ix−1I<3 i Ix−1I>1 (x−1<3 i x−1>−3) i (x−1>1 lub x−1<−1)

Aga1: Zrobiłabym tak Ix−1I−2<1 i Ix−1I−2>−1 Ix−1I<3 i Ix−1I>1 x∊(−2,4) i x∊(−∞,0)∪(2,∞) część wspólna , odp.(−2,0)∪(2,4)

DużeK: dobra panowie i panie, głupota, przemęczenie, czy coś w tym stylu, dzięki za szybkie odpowiedzi. Wychodzi na to że niewiele wiem a matura za pasem, Jeszcze raz dzięki

Mila: DUZEK rozwiąż graficznie! Funkcje wdzięczne do rysowania, punkty przecięcia to punkty kratowe.

Eta: Ojj tak, tak i co to będzie?

Mila: Que, sera,sera.

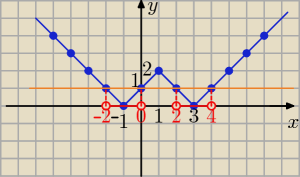
Eta: Odp: x€ ( −2,0) U (2,4)