objętość stożka jest równa V, a tworząca stożka jest nachylona do płaszczyzny po malaga: Proszę o pomoc, o jakąś wskazówkę . objętość stożka jest równa V, a tworząca stożka jest nachylona do płaszczyzny podstawy pod kątem α. Wyznacz objętość kuli wpisanej w ten stożek.

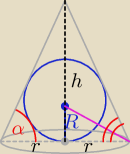
think: znamy tylko objętość stożka i kąt jaki tworzy tworząca z podstawą. r − oznacza promień podstawy stożka R − promień kuli

	1
V =		πr2h
	3

	h
tgα =
	r

więc możesz sobie wyliczyć r lub h. co do kuli to przekrój to będzie okrąg wpisany w trójkąt równoramienny, a okrąg można wpisać w trójkąt w punkcie przecięcia dwusiecznych kątów.

	α		R
Zatem tg		=
	2		r

rumpek: Rysunek: http://images49.fotosik.pl/1352/eff848a331e618a8.jpg Rozwiązanie:

	1		1
* wzór na objętość stożka: V =		* Pp * H ⇔ V =		πr2H
	3		3

	4
* wzór na objętość kuli: V =		πR3
	3

To z rysunku, wyznaczamy wysokość (na podstawie definicji trygonometrycznych)

	H
tgα =		/ * r
	r

H = rtgα

	πr2 * rtgα		πr3tgα
V =		=
	3		3

3V = πr³tgα / : tgα

	3V
πr3 =
	tgα

	3V
r3 =
	tgαπ

Zapomniałem na rysunku umieścić jednej wielkości − mianowicie promienia kuli − R, powinien to być odcinek |AE|.

	α		R
tg		=
	2		r

	α
R = tg		r
	2

Pole kuli:

	4
V =		πR3
	3

	4		α		3V
V =		πtg3		*
	3		2		tgαπ

	α   4Vtg3   2
V =
	tgα

luki: Według mnie jest tu błąd. Gdyż wartości R nie podniosłeś do potęgi 3