 Witam, miałam zadanie i rozwiązałam je "na czuja", wiem czy dobrze i chciałabym, żeby ktoś mi
powiedział co o tym sądzi.
Zad: Napisz wzór funkcji liniowej, której wykres jest nachylony do dodatniej półosi OX pod
kątem α=34π i przechodzi przez punkt P=(−1,7)
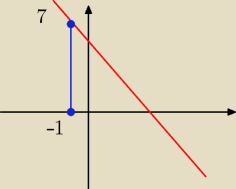
Narysowałam sobie wykres i wyszło, że powstały trójkąt jest trójkątem 45,45,90, więc:
0=6a+b
7=−a+b
wyszło mi y=−x+6
Czy to dobra odpowiedź?
Jeszcze mam podpunkt b, za który nie wiem jak się zabrać. : Jaką wartość musi mieć parametr k,
aby prosta o równaniu y=|k+1|x−3 przecinała wykres funcji z punktu a pod kątem prostym.
Witam, miałam zadanie i rozwiązałam je "na czuja", wiem czy dobrze i chciałabym, żeby ktoś mi
powiedział co o tym sądzi.
Zad: Napisz wzór funkcji liniowej, której wykres jest nachylony do dodatniej półosi OX pod
kątem α=34π i przechodzi przez punkt P=(−1,7)
Narysowałam sobie wykres i wyszło, że powstały trójkąt jest trójkątem 45,45,90, więc:
0=6a+b
7=−a+b
wyszło mi y=−x+6
Czy to dobra odpowiedź?
Jeszcze mam podpunkt b, za który nie wiem jak się zabrać. : Jaką wartość musi mieć parametr k,
aby prosta o równaniu y=|k+1|x−3 przecinała wykres funcji z punktu a pod kątem prostym.
| 3 | ||
α= | π | |
| 4 |
 proste o równaniach y=ax + b i y=cx +d są PROSTOPADŁE, gdy:
a*c = −1
proste o równaniach y=ax + b i y=cx +d są PROSTOPADŁE, gdy:
a*c = −1 
