Liczba rozwiązań w zależności od parametru MvC: Wyznacz liczbę rozwiązań równania w zależności od parametru a: a² + | |x+1| − 1| = 1 Rozw: 0, dla x∊ (−∞, −1) lub (1, +∞) 1, dla x∊ {−1,1} 2, dla x = 0 3, dla x∊ (−1,0) lub (0,1)

Mila: Najlepiej rozwiąż graficznie równanie: ||x+1|−1|=1−p² W razie wątpliwości pytaj.

MvC: No to opuściłem tą wartośc bezwzględną w środku i mam 1. dla x ≥−1 |x| = −a² +1 2. dla x < −1 | −x −2| = −a² + 1 czyli −x −2 = −a² +1 lub −x −2 = a² −1 i tylko dla tego ostatniego rownania przecinaja mi sie wykresy w dwoch punktach. A w odpowiedziach są punkty z 3 czy 4 rozwiazaniami. Jak to trzeba zrobić? ...

MvC: podbijam w górę...

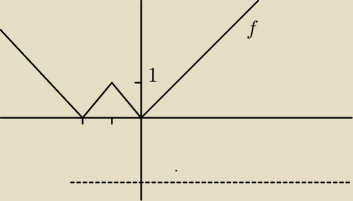
Mila: f(x) =||x+1|−1| y=1−a² 1−a² <0 brak rozwiązań 1−a² =0 dwa rozwiązania 0<1−a² <1 cztery rozwiązania 1−a² =1 trzy r 1−a² >1 dwa r