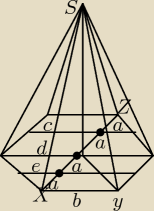
stereo zbk: w ostrosłupie prawidłowym sześciokątnym o wierzchołku S na najdłuższej przekątnej XZ podstawy obrano 3 punkty które podzieliły tę przekątną na cztery równe części.Przez punkty podziału poprowadzono płaszczyzny równoległe do ściany bocznej SXY.Oblicz stosunek pól otrzymanych 3 przekrojów tego ostrosłupa

	b+2b
moje obliczenia c=		d=2b e=c prosze o pomoc mam kłopot z
	2

wyobrażeniem sobie tych płaszczyzn i wyliczenem ich pól myśle że będą to trapezy ale nie mam pewności

Artur z miasta Neptuna: powstanie trapez ... trójkąt ... taki sam trapez co wcześniej zakładam, że 'd' dobrze wyliczyłeś, wtedy 'c' jest dobrze wyliczone (jedno z tw. trapezu się wykorzystuje)

Artur z miasta Neptuna: h_trójkąta = H_ostrosłupa (niewiadoma)

	1
htrapezu =		htrójkąta −−− z podobieństwa trójkątów vel tw. Talesa
	2

	1
F // górna podstawa trapezu // =		b −−− z podobieństwa trójkątów vel tw. Talesa
	2

(identyczy rysunek co do wyższego) i podstawiasz.

zbk: ale czy pole trapezu z dolną podstawą e będzie równe polu trapezu z podstawą c przecież jak one są równoległe do ściany XYS to są pochylone w kierunku ściany leżącej naprzeciwko XYS pod takim samym kątem co XYS przynajmniej tak mi się wydawało

zbk: i czy dobrze zrozumiałem płaszczyzna oparta na krawędzi d to bedzię trójkąt? i czy równoramienny jak tak to też ten trójkąt jest pochylony pod takim samym kątem do podstawy jak ściana XYS a wtedy htrójkąta nie = H ostrosłupa

zbk: wiem że mają powstać dwa trapezy i jeden siedmiokąt