Dany jest okrąg Mati: Dany jest okrąg O: x²+y²−8x−2y+1=0 i prosta m: 2x − y + 2=0. Znajdź równanie okregu O', stycznego do prostej m i przechodzącego przez środek okręgu O, jeśli wiadomo, że środek okręgu O' leży na prostej o równaniu x−y=0 . Z góry dziękuje za pomoc.

Mati: pomocy

Beti: najpierw analizujemy dany okrąg O: wyznaczamy jego środek, czyli powiedzmy pkt S=(a,b)

ejendi: trochę na skróty m: jest styczna do O; pkt.A(0.4,2.8) czyli O' jest w tym pkt. styczny do O i m liczę ale jakoweś "gupoty" wychodzą, może już ktoś rozwiązał? gdzieś robię bład

Beti: a gdzie w zad. przeczytałeś, że m jest styczna do O? Ona jest styczna do O'

ejendi: wiem, wiem to był bład, jakoś wrednie się liczy bo są ułamki wyszło, że ⊥ do m przez Oo(4,1) jest y=−1/2x+3 przecięcie jej z m to A(2/3,2 1/3) teraz odległość A Oo i |A Oo| to 2r wsp. środka z Oo(4,1) i A(2/3,2 1/3)

Beti: ale mi żadne ułamki nie wyszły za to równ. okręgu wyszło takie: (x−3)²+(y−3)²=5

Mati: odpowiedz powinna byc: O': (x−3)²+(y−3)²=5

Beti:

Mati: ale dalej nie wiem skąd to wyszlo

Beti: mogę Cię naprowadzać, ale liczyć musisz sam.

Mati: wiec proszę o jakąś podpowiedz, bo wcześniejsza nic mi nie dała

Beti: wyznacz współrz. środka okręgu O

Mati: O(4,1)

Beti: OK S=(4,1) teraz dalej: Srodek okręgu O' leży na prostej y=x, czyli jak ogólnie można zapisać współrzędne środka S'?

Mati: S' (x,x)

Beti: czyli S' = (a,a) → skoro wsp. spełniają warunek y=x, to obie wsp. są sobie równe Dalej: środek okręgu O' leży na prostej i okrąg ten przechodzi przez Srodek okr. O, czyli pkt S=(4,1). Zatem |SS'| = r' Ale też okrąg O' jest styczny do prostej m, więc d(S',m)=r' Wyznacz |SS'| oraz d(S',m) i przyrównaj je do siebie − dostaniesz równanie kwadratowe, z którego wychodzi a=3.

Beti: zamień x na a, żebyś widział, że liczysz współrzędne Srodka okręgu

Mati: dobrze. zaraz spróbuje bardzo dziękuje

Mati: wyszlo. jeszcze raz bardzo dziekuje

Beti: na zdrowie

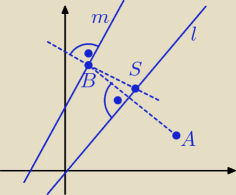
ejendi: wracam do sprawy, poprzednio się zapętliłem, może to się spodoba? l:y=x m:y=2x+2 A(4,1) środek okręgu B(1,4) symetria wzgledem y=x BS ⊥ do m: przez B czyli y=2x+2 ⊥ do y=−1/2x+b przez B y−4=−1/2(x−1); y=−1/2x+4 1/2 przecięcie z l: y=x −1/2x+4 1/2=x 3/2x= 4 1/2 x=3 i y=3 ⇒S(3,3) BS=(1−3,4−3)=(−2,1) r=|BS|=√4+1=√5 równanie okręgu (x−3)²+(y−3)²=5