Ekstema lokalne
Tiamat: Mógłby mi ktoś wypisać co po kolej robić, żeby rozwiązać zadanie o takiej treści: "wyznaczyć
ekstrema lokalne oraz przedziały monotoniczności funkcji" ?
Daję przykład, żeby dało się zrobić wizualizację:
f(x) = x2 + 8x
27 lut 12:51
Aga1: Licz dziedzinę , pochodną, pochodną przyrównaj do zera
f'>0 f'<0
27 lut 12:57
Tiamat: ok, zatem:
x ≠ 0 czyli D: R \ {0}
i to porównanie będzie chyba wyglądało jakoś tak:
Nie wiem, co dalej? Btw, zawsze mam liczyć dziedzinę?;3
27 lut 13:06
Aga1: Zawsze.
Pochodną źle obliczyłeś, popraw
Oblicz miejsca zerowe pochodnej, pomnóż obie strony przez mianownik
27 lut 13:13
ICSP: Aga1 czy będzie różnica w liczeniu pochodnej jeśli najpierw przekształcę tą funkcję(np.
sprowadzę do wspólnego mianownika)?
27 lut 13:15
Tragos: nie jestem Aga, ale odpowiem nie

27 lut 13:16
ICSP: Dziękuję bardzo

27 lut 13:17
Tragos: | | f | |
tutaj licząc pochodną, nie ma po co używać wzoru na ( |
| )'  |
| | g | |
| | x | | 8 | | 1 | | 1 | | 1 | | −1 | | 1 | | 8 | |
f(x) = |
| + |
| = |
| x + 8 |
| = |
| + 8 |
| = |
| − |
| |
| | 2 | | x | | 2 | | x | | 2 | | x2 | | 2 | | x2 | |
27 lut 13:20
Aga1: Witaj ICSP, to Twoje zadanie, czy tylko się zapytałeś?
27 lut 13:21
ICSP: To było z ciekawości

Moje zadanie wygląda troszkę inaczej

27 lut 13:23
Tiamat: Chodzi o to że nie skróciłam 24 do 12? : D
Bo jeśli to coś innego to nie mam pojęcia gdzie jest błąd:3
27 lut 13:24
Tiamat: Ale jak chcę to mogę używać tego wzoru? Bo mi łatwie trzymać się jednej metody, niż każdą
pochodną liczyć różnymi sposobami.
27 lut 13:25
27 lut 13:26
Aga1:
U P[U[Tragosa]] powinno być f
'=
x
2−16=0
x=−4, x=4 są to punkty podejrzane o ekstremum
27 lut 13:26
Tragos: rzeczywiście, widzę zaszalałem z zapisem

| | x | | 8 | | 1 | | 1 | |
f(x) = |
| + |
| = |
| + 8 |
| |
| | 2 | | x | | 2 | | x | |
a reszta to już f'(x)

27 lut 13:29
Tiamat: Czyli moge se wsadzić ten wzór, bo mi znaki inaczej wyszły: /
Masakra xD
27 lut 13:30
Tragos: nie.. ten wzór jest dobry.. powinno wychodzić tak samo, zaraz przeliczę
na pewno stosujesz go w formie:
| | f | | f'g − fg' | |
( |
| )' = |
| = ? |
| | g | | g2 | |
27 lut 13:32
Tiamat: No właściwie to pochodną zawsze daję na początek, czyli mniej więcej coś takiego:
ale na jedno wychodzi:3
27 lut 13:37
Tragos: | | x | | 8 | | x2 + 16 | |
f(x) = |
| + |
| = |
| |
| | 2 | | x | | 2x | |
| | x2 + 16 | | (x2 + 16)' * 2x − (2x)' * (x2 + 16 | |
f'(x) = ( |
| )' = |
| = |
| | 2x | | (2x)2 | |
| 2x * 2x − 2x2 − 32 | | 4x2 − 2x2 − 32 | | 2x2 − 32 | | 2 | |
| = |
| = |
| = |
| − |
| 4x2 | | 4x2 | | 4x2 | | 4 | |
wychodzi to samo

27 lut 13:41
Tiamat: a widzisz, ja tego nie skleiłam w jeden ułamek tylo liczyłam
(x2)' + (8x)
pewnie dlatego
27 lut 13:44
Tiamat: zgubiłam prim:3
27 lut 13:44
Aga1: Jakby nie liczyć to wynik wychodzi taki sam.
27 lut 13:47
Aga1: Tragos pomagaj dalej , ( jak się wciąłeś)
27 lut 13:49
Tiamat: Ok, czyli mam przyjąć, że coby tam nie było i tak wyjdzie na jedno?

Czyli teraz robie porównanie, tak?
Ok, czyli
x= −4 i x=4 i to są nasze potencjalne ekstrema tak?:3
27 lut 13:54
Tragos: ja tylko chciałem pokazać inny sposób liczenia pochodnej, po co stosować taki wzór do takiej
pochodnej

licząc dowolnym sposobem tą pochodną wyjdzie to samo
f'(x) = 0
x = −4 lub x = 4
i to są punkty podejrzane o ekstremum
rozwiąż teraz
f'(x) > 0 oraz f'(x) < 0
27 lut 13:57
Tiamat: Ok, wyszło mi to samo: x=−4 oraz x=4
W zasadzie, zastanawiam się po co to liczyć, jeśli wychodzi to samo?;3
27 lut 13:59
Tragos: rozwiąż f'(x) > 0 i f'(x) < 0

27 lut 14:09
Tiamat:
x> −4
x<4
?
27 lut 14:14
Tragos: f'(x) > 0 ⇔ x ∊ (−∞, −4) u (4, ∞)
z tego wynika, że funkcja jest rosnąca w przedziałach
(−∞, −4) oraz (4, ∞)
−−−−−−−−−−−−−−−−−−−−−−−−−
f'(x) < 0 ⇔ x ∊ (−4, 4) / {0}
z tego wynika, że funkcja jest malejąca w przedziałach
(−4, 0) oraz (0, 4)
−−−−−−−−−−−−−−−−−−−−−−−−−
teraz sprawdzamy te ekstrema
dla x = −4, będzie ekstremum lokalne maksymalne, bo znak pochodnej zmienia się z plusa na minus
dla x = 4, będzie ekstremum lokalne minimalne, bo znak pochodnej zmienia się z minusa na plus
27 lut 14:17
Tiamat: Matko ale to skomplikowanie wygląda, myślałam że to będzie nieco łatwiejsze: D
Ok, mam to podstawić do pochodnej?
I co dalej, po kolei? Tak mniej więcej, bo muszę się zbierać, więc razem nie policzymy:3
27 lut 14:25
Tragos: jak co dalej?

to już koniec zadania
27 lut 14:28
27 lut 14:29
Aga1: Wtrącę się, ekstrema trzeba teraz wyznaczyć licząc ze wzoru podanej funkcji
ymax=f(−4)=
iymin=f(4)= f(4)=
27 lut 14:52
Tiamat:
ok, to się zgadza, jakby wyglądała tabelka i jak sformuować odpowiedź? Bo moja babka odejmuj
pkt jak nie ma odpowieedzi

28 lut 10:52
Aga1: Taka odpowiedź, jakie pytanie, czy polecenie.
A co do tabelki, to zrób szkic (bo różnie są robione) i pomogę Ci ją uzupełnić, jeśli nie
będziesz wiedziała.
28 lut 10:58
Artur z miasta Neptuna:
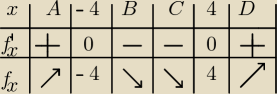
tak może wyglądać tabelka:
legenda:
f'
x = f'(x)
f
x = f(x)
A = (−
∞,−4)
B = (−4,0)
C=(0,4)
D = (4,+
∞)
chyba w tabelce nie zaznacza się asymptot pionowych (x=0), ale to musisz sprawdzić.
28 lut 11:11
Tiamat: Rysowanie tutaj to koszmar xD
Ok to może tak:
l (−∞,−4) l (−4) l (−4,4) l (4) l (4,∞)
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
f'(x) l + l 0 l − l 0 l +
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
f(x) l Rośnie l max l Maleje l min l Rośnie
No tam powinny być strzałki:
Rośnie skierowane w prawy róg górny
Maleje skierowane w prawy dolny róg
:3
28 lut 11:14
Tiamat: Buuu, czemu tam ma być zero? I skąd je wziąć w innych przypadkach?

28 lut 11:14
Artur z miasta Neptuna:
gdzie zero

jakie 0 ? o czym Ty mówisz?
28 lut 11:22
Tiamat: Odpowiedź: funkcja ma estrema lokalne −4 oraz 4 oraz jest rosnąca w przedziałach: (−∞,−4) i
(4,∞0), a malejąca w (−4,4).
Dobrze to ujęcłam?:3
28 lut 11:22
Artur z miasta Neptuna:
hmmm ... patrz: 'dziedzina funkcji'

28 lut 11:22
Tiamat: To w tabelce, ale chyba już wiem, to jest asymptota po prostu?
28 lut 11:23
Tiamat: Czyli do tabelki muszę wrzucić też to co wcześniej "wyrzucam" ?
28 lut 11:23
Artur z miasta Neptuna:
inaczej −−− w tabelce musi być informacja jak się funkcja zachowuje DLA KAŻDEGO X∊R ... więc
jeżeli jakiś 'x' ∉ Df ... to musi być o tym wzmianka w tabelce
bo to co Ty napisałeś oznaczałoby, że f(0) istnieje, co jest oczywiście bzdurą
28 lut 11:29
Tiamat: Nie nie, chyba to po prostu debilnie napisałam: D
Ale rozumiem raczej o co Ci chodzi, musi być ale właćiwie nie ma. Jakby.
28 lut 11:30




 Moje zadanie wygląda troszkę inaczej
Moje zadanie wygląda troszkę inaczej 



 Czyli teraz robie porównanie, tak?
Ok, czyli
x= −4 i x=4 i to są nasze potencjalne ekstrema tak?:3
Czyli teraz robie porównanie, tak?
Ok, czyli
x= −4 i x=4 i to są nasze potencjalne ekstrema tak?:3
 licząc dowolnym sposobem tą pochodną wyjdzie to samo
licząc dowolnym sposobem tą pochodną wyjdzie to samo

 to już koniec zadania
to już koniec zadania

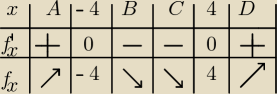 tak może wyglądać tabelka:
legenda:
f'x = f'(x)
fx = f(x)
A = (−∞,−4)
B = (−4,0)
C=(0,4)
D = (4,+∞)
chyba w tabelce nie zaznacza się asymptot pionowych (x=0), ale to musisz sprawdzić.
tak może wyglądać tabelka:
legenda:
f'x = f'(x)
fx = f(x)
A = (−∞,−4)
B = (−4,0)
C=(0,4)
D = (4,+∞)
chyba w tabelce nie zaznacza się asymptot pionowych (x=0), ale to musisz sprawdzić.

 jakie 0 ? o czym Ty mówisz?
jakie 0 ? o czym Ty mówisz?
