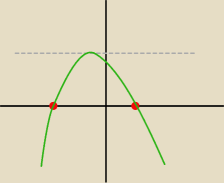
pomocy bcq: Funkcja kwadratowa f przyjmuje największą wartość równą 3¹₅, a zbiorem nierówności f(x) > 0 jest przedział (−5,3). Wyznacz wzór funkcji f w postaci ogólnej. Jak to wyznaczyć?

Tragos: a < 0 f(x) = a(x + 5)(x − 3) = a(x² − 3x + 5x − 15) = a(x² + 2x − 15) = ax² + 2ax − 15a

	−2a
p =		= −1
	2a

	1
f(−1) = 3
	5

podstaw tutaj i oblicz a

asdf: q = 3 i cos tam co napisał

	x1 + x+2
p =
	2

y = a(x − p)² + q f(0) = −5 f(0) = 3

asdf: f(−5) = 0 f( −1) = 3 i cos tam f( 3) = 0

asdf: a....jak chcesz postac ogolna to rozpisz (x − p)²

pigor: ... lub z warunków zadani masz p=⁻⁵⁺³₂=−1 , czyli f(x)=a(x+1)+3¹₅ i np. f(3)=0 ⇒ a*4+¹⁶₅=0 ⇔ 20a=−16 ⇔ a= −⁴₅ , zatem f(x)= ⁴₅(x²+2x+1)+¹⁶₅ = ⁴₅x²+⁸₅x+²⁰₅ . ...