całka z Krysickiego marek: ∫₀^a dx∫₀^b(1−x/a) √1−(x/a)² −(y/b)² dy

Trivial: 0 ≤ x ≤ a

	x
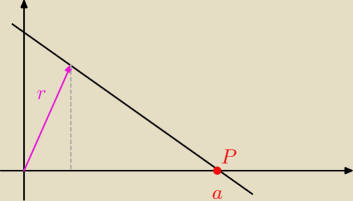
0 ≤ y ≤ b(1−		)
	a

Natychmiast przechodzimy na współrzędne eliptyczne.

	⎧	x = arcosφ
Φ:	⎨
	⎩	y = brsinφ

JacΦ = abr (chyba) Nasz punkt przecięcia P spełnia oba równania na raz, tj.: x = a

	a
y = b(1−		) = 0.
	a

Zatem

	π
0 ≤ φ ≤
	2

Pozostało wyliczyć granice r. Podstawiamy do równania nasze współrzędne.

	x
y = b(1−		)
	a

	arcosφ
brsinφ = b(1−		)
	a

rsinφ = 1−rcosφ r(sinφ+cosφ) = 1

	1		1
r =		=
	sinφ+cosφ		sinφ+cosφ

Zatem

	1
0 ≤ r ≤
	sinφ+cosφ

Ta całka = ∫_0..π/2dφ∫_{0..1/(sinφ+cosφ)} √1−r²*abr dr = ... ← prosta całka

marek: w sumie nie wiem czemu ale zapomniałem o przejściu na współrzędne eliptyczne... Pierwszą całkę łatwo dało się wyliczyć, jednak już tą drugą z arcsin itp ciężko było...

Trivial: Teraz tak myślę, czy rzeczywiście będzie prościej w ten sposób.