Prawdopodobieństwo Szprot: Zadanie 1.9a Rzucamy dwiema kostkami do gry. Obliczyć prawdopodobieństwo wyrzucenia więcej niż 3 oczek na pierwszej kostce, jeśli wiadomo, że suma oczek na obu kostkach jest mniejsza od 5. Zadanie 1.9b Rzucamy dwiema kostkami do gry. Obliczyć prawdopodobieństwo wyrzucenia więcej niż 3 oczek na pierwszej kostce, jeśli wiadomo, że suma oczek na obu kostkach jest mniejsza od 6. Zadanie 1.10 53% studiujących w pewnej uczelni to panie. Wiadomo, że 9% pań i 12% panów nie zaliczyło sesji w tej uczelni. Obliczyć prawdopodobieństwo, ze losowo wybrany student z tej uczelni nie zaliczył sesji. Zadanie 1.11 Każda z trzech urn zawiera 6 czerwonych i 4 białe kule. Z pierwszej urny losowo wybieramy jedn ą kulę i przekładamy do drugiej urny. Następnie z drugiej urny losujemy jedną kulę i przekładamy do trzeciej urny. Obliczyć prawdopodobieństwo wylosowania z trzeciej urny kuli białej. (odp. 0). 1.9a (odp. 0,1). 1.9b (odp. 0,1041). 1.10 (odp. 0,4). 1.11 Chciało by się komuś rozwalić któreś z zadań tłumacząc co nie co Kuleję z prawdopodobieństwa a dużo by mi pomogło na uczelni żebym miał to na jutro rozwiązane. Może i sam bym to rozwiązał ale kompletnie nie mam czasu gdyż poprawki męczę

Szprot: bump!

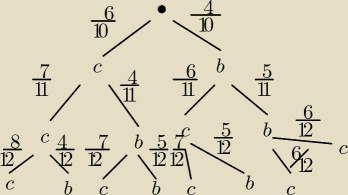
Janet: Zadanie 1.11 Zrobiłam z drzewka,

	6		7		4		6		4		5		4		6		5
P(A) =		*		*		+		*		*		+		*		*
	10		11		12		10		11		12		10		11		12

	4		5		6		528		2
+		*		*		=		=		= 0,4
	10		11		12		1320		5

Janet: oj, na ostatniej gałązce z prawej strony ma być oczywiście "b" a nie "c"..

Mila: 1,9a) Rzucamy dwiema kostkami Ω=36 A− na pierwszej kostce wypadło więcej niż 3 oczka B− suma oczek na obu kostkach jest mniejsza od 5 B={(1,1),(1,2),(1,3) (2,1),(2,2),(3,1)} |A∩B|=0

	0
p(A/B)=		=0
	6

Mila: Rzucamy dwiema kostkami Ω=36 A− na pierwszej kostce wypadło więcej niż 3 oczka B− suma oczek na obu kostkach jest mniejsza od 6 B={(1,1),(1,2),(1,3),(1,4) (2,1),(2,2),(2,3)(3,1),(3,2),(4,1)} |B|=10 A∩B ={(4,1)} |A∩B|=1

	1
P(A/B)=
	10

Mila: 1,10 N − nie zaliczona sesja K− wybrano kobietę M− wybrano Mężczyznę P(N)=P(K)*P(N/k)+P(M)*P(N/M)= P(N)=0,53*0,09+0,47*0,12

Szprot: Dziękuję serdecznie

Mila:

kRIS: Rzucamy dwiema kostkami Ω=36 A− na pierwszej kostce wypadło więcej niż 3 oczka B− suma oczek na obu kostkach jest mniejsza od 5 B={(1,1),(1,2),(1,3) (2,1),(2,2),(3,1)} |A∩B|=0 0 p(A/B)=0/6 = 0 Ktoś może to dokładniej opisać Czy to jest liczone z prawd. warunkowego? Jeżeli tak to skąd ta 6 w mianowniku?