stereometria
Ania: Ostrosłup prawidłowy trójkątny przecięto płaszczyzną zawierającą wysokości dwóch ścian bocznych
poprowadzone z wierzchołka ostrosłupa. Wiedząc, że otrzymany przekrój jest trójkątem
równobocznym o boku 6, oblicz objętość tego ostrosłupa
26 lut 19:56
asdf:
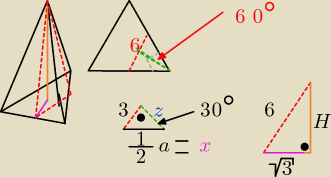
x = 6
a = 12
Pp = 36
√3
h = 3 √3
| | 1 | | 1 | |
wysokość ostrosłupa pada na |
| wysokości podstawy od |
| a ( trójkąt po lewej) |
| | 3 | | 2 | |
H ostrosłupa =
√33
26 lut 20:23
asdf: (trójkąt po lewej) − pomyłka − ten po prawej
26 lut 20:24
asdf: sprawdzi to ktoś?
26 lut 20:25
asdf: REF
26 lut 20:33
asdf: sprawdźcie prosze, bardzo mi zalezy bo niedlugo mam prace klasowa z ostroslupow (i
graniastoslupow)
26 lut 20:44
asdf: ...

sprawdzcie to prosze
26 lut 21:06
Ania:

czerwony trójkąt jest równoboczny? jesteś pewien?
26 lut 21:12
Ania: wszystko się zgadza według mnie, dziękuję wychodziło mi podobnie. ; )
26 lut 21:13
Ania: ale objętość źle liczysz.
w podstawie jest trójkąt równoboczny czyli a2√3/4
V=1/3 * 144√3/4 * √33
V=12√3 * √33
V=12√99
V=36√11
26 lut 21:19
asdf: no tak...pomylilem wzory (n−ty raz juz)
26 lut 21:23
Ania: jeszcze się upewnię, i dam zaraz znać, czy dobrze myślimy. ; )
26 lut 21:26
asdf: ok
26 lut 21:31
Ania: wszystko jest okej. ; ) Pozdrawiam
26 lut 21:51
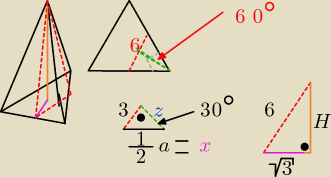
 sprawdzcie to prosze
sprawdzcie to prosze
 czerwony trójkąt jest równoboczny? jesteś pewien?
czerwony trójkąt jest równoboczny? jesteś pewien?