 dany jest trapez równoramienny o podstawach AB=a i CD=b gdzie (a>b).
dany jest trapez równoramienny o podstawach AB=a i CD=b gdzie (a>b).
| a+b | ||
Odcinek DE jest wysokością tego trapezu . Wykaż ,że EB= | . | |
| 2 |
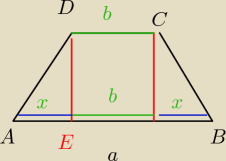 2x+b=a
2x=a−b//:2
2x+b=a
2x=a−b//:2
| a−b | ||
x= | ||
| 2 |
| a−b | 2a | a+b | a+b | |||||
IEBI=a−x=a− | = | − | = | . | ||||
| 2 | 2 | 2 | 2 |
| 2b | a−b | 2b−b+a | a+b | |||||
IEBI=b+x= | + | = | = | |||||
| 2 | 2 | 2 | 2 |
| 2a−a+b | ||
IEBI= | ( na jednej kresce) | |
| 2 |
