planimetria nika: proszę o pomoc dany jest trójkąt równoramienny ABC o ramionach AC,BC i podstawie AB. na prostej AB zaznaczono na zewnątrz trójkąta punkty E,F , takie że AE=BF. wykaż że trójkąt EFC jest równoramienny.

nika: pomocy....

pigor: ... otóż ΔBFC=ΔBEC − trójkąty przystające z II cechy przystawania trójkątów (bkb) , gdzie ∡FBC=∡EAC jako kąty przyległe do równych kątów przy podstawie danego ΔABC − równoramiennego i to tyle . ...

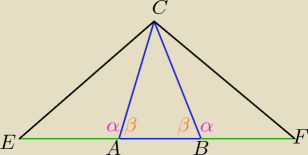
Eta: ΔEAC przystaje do ΔBFC z cechy ( b,k,b) to: |EC|= |FC| ⇒ ΔEFC jest równoramienny