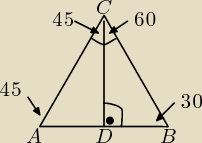
 W trójkącie wysokość opuszczona z wierzchołka C trójkąta ABC dzieli kąt ACB na kąty o miarach
45 i 60 stopni. Wiedząc, że odcinek AB=12cm, oblicz pole trójkąta ABC.
Zacząłem to robić tak:
No i obliczyłem z funkcji trygonometrycznych dla trójkąta prostokątnego długości boków AC=4√3
i BC = 6√2
Niestety później z twierdzenia Pitagorasa wychodzi mi różna wysokość inna w △ADC inna w ΔBDC.
Będę bardzo wdzięczny za pomoc w rozwiązaniu tego zadania
W trójkącie wysokość opuszczona z wierzchołka C trójkąta ABC dzieli kąt ACB na kąty o miarach
45 i 60 stopni. Wiedząc, że odcinek AB=12cm, oblicz pole trójkąta ABC.
Zacząłem to robić tak:
No i obliczyłem z funkcji trygonometrycznych dla trójkąta prostokątnego długości boków AC=4√3
i BC = 6√2
Niestety później z twierdzenia Pitagorasa wychodzi mi różna wysokość inna w △ADC inna w ΔBDC.
Będę bardzo wdzięczny za pomoc w rozwiązaniu tego zadania 
| CD | |
= tg 45o = 1
| |
| AD |
| CD | AD | √3 | |||
= | = tg 30o = | ||||
| DB | 12−AD | 3 |
| 12√3 | ||
AD = CD = | ||
| 3+√3 |
| AB*CD | ||
S = | = ........ = 36(√3−1) | |
| 2 |