x − argumenty
y − wartości
a= −2 więc ramiona w doł
y = −2(x2 − 5x −x + 5)
y = −2x2 + 12x − 10
Δ = b2 − 4ac
Δ = 144 − 80
Δ = 64
Wierzchołek składa się z dwóch współrzędnych p − wartość x; q − wartość y
określeniem największego punktu na osi będzie wierzchołek paraboli
| −Δ | ||
q = |  | |
| 4a |
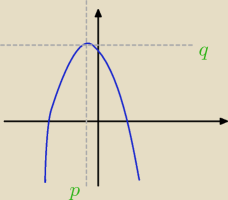mniej wiecej tak bedzie wygladac rysunek
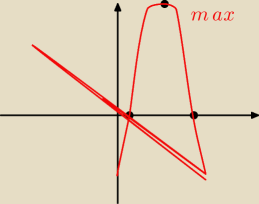
| −Δ | ||
max=yw= | ||
| 4a |