planimetria xxxxxxxxxxxxx: punkt O jest środkiem okręgu wpisanego w trójkąt równoramienny o podstawie AB. punkt S jest środkiem okręgu opisanego na tym trójkącie. wiadomo, że |AB|=6, |AC|=5. oblicz długość promieni okręgów o środkach w punktach O i S.

Eta:

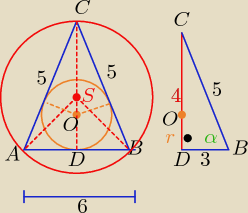
	1
Z tw. Pitagorasa h=4 rw=		h =...........
	3

	4
sinα=
	5

	5
ze wzoru sinusów w ΔABC		= 2R ⇒ R=.........
	sinα

Eta: Sorry −−− trójkąt równoramienny to:

	2P
rw=		P= 12 p= 16
	p

	24
rw=		= ............
	16

reszta ok

xxxxxxxxxxxxx: skąd się bierze P i p ?

Eta:

	1
P=		a*h= ............. = 12
	2

p= Ob = a+b+b =........ = 16

xxxxxxxxxxxxx: 24, 16 i 1,5 to długość promieni?

Eta: Tak r_w= 1,5 teraz tylko oblicz: R= ..........

xxxxxxxxxxxxx: a jaki jest wzór na R?

Eta: Omg przecież Ci podałam jak na tacy ze wzoru sinusów

	5		4
2R=		sinα=
	sinα		5

to:

	5
2R=
	4   5

	5
2R= 5*
	4

	25
2R=
	4

	25
R=		= .........
	8

xxxxxxxxxxxxx: pomoz mi w innych zadaniach z planimetri, ktore podalam