pochodne monotonicznosc ekstremum donde: Witam. Mam podaną funkcję y = x * ln (x) i mam wyznaczyć: 1. dziedzinę 2. miejsca zerowe 3. parzystość nieparzystość 4. asymptoty 5. monotoniczność 6. ekstremum 7. punkty przegięcia 8. wypukłość wklęsłość 9. tabelka i wykresy No więc tak 1. Dziedzina R>0 2. Ln (x) = 0 czyli x=1 3. No to nie jest funckja parzysta, ani nie parzysta. No i dalej się zaczynają schody. Wyliczyłem pierwszą pochodną ( x * ln (x) )' = ln x + 1 ale nie wiem dalej niestety jak to ma być, liczę na pomoc

Aga1: Poprawka. 1.x>0 czyli D=R⁺ 2. x*lnx=0 x=0 lub lnx=0 x=1

Grześ: Teraz pomyśl nad jakimiś asymptotami, pokaż obliczenia, będę poprawiał w razie czego

donde: No zgadza się x>0 wiec dziedzina to rzeczywiste dodatnie, ale w drugim x=0 nie moze byc poniewaz nie należy do dziedziny (mimo że teoretycznie wychodzi − wiadomo). Ale kompletnie nie wiem jak ugryźć następne punkty.

Grześ: parzystośc i nieparzystość − sprawdzasz najpierw czy dziedzina jest przedziałem symetrycznym (x∊D ⋀ −x∊D) Jak widać taki nie jest wic nie ma adnej takiej własności Teraz sprawdzaj asymptoty ( ukosne, pionowe )

Aga1: Oczywiście x=0 nie jest miejscem zerowym funkcji , bo nie należy do dziedziny, ale zapisać rachunki trzeba. 4 lim_x→0⁺xlnx=0 Prosta o równaniu x=0 jest asymptotą pionową prawostronną wykresu.

donde: Skoro to całe wyrażenie x * lnx przy liczeniu granicy dąży do 0 to prosta x=0 jest asymptotą pionową, ale nie czasem lewostronną (ponieważ na lewo od 0 nic się nie znajduje już)

Aga1: Po lewej stronie 0 funkcja nie jest określona, więc nie liczymy lim_x→0⁻ Wykres będzie znajdował się po prawej stronie tej asymptoty.

donde: No faktycznie (myślałem że oznaczenie jest na odwrót). Ale dalej nie wiem jak za resztę się wziąć...

Aga1: licz lim_x→∞xlnx=∞, nie ma asymptoty poziomej asymptota ukośna

	1
limx→∞ xlnx*		=∞
	x

Nie ma asymptoty ukośnej. 5. Pochodną dobrze policzyłeś. f^'>0 f<0

donde: ln x + 1 > 0 ln x > −1 lnx = −1 e⁻1 = x x = 1/e f'> 0 dla x> 1/e f'< 0 dla x< 1/e

Aga1:

	1
Funkcja jest rosnąca dla x>
	e

	1
Funkcja jest malejąca dla x∊(0,		)
	e

6. ekstremum

	1
ymin=f(		)=
	e

7. licz drugą pochodną.

donde: Mam małe pytanie teraz. Ten ln odnosi się do całości x + 1 czy samego x, żebym głupoty nie palnął.

Aga1: ln odnosi się tylko do x, gdyby było inaczej to zapis wyglądałby tak ln(x+1)

donde: ok w takim razie będzie ((ln x) + 1)' = 1/x

Aga1: Ok . Ekstremum policzyłeś?

donde: Ekstremum? No właśnie teraz nie wiem, bo żeby policzyć punkty przegięcia przyrównuje się do 0 drugą pochodną. Czyli 1/x =0 no i z tego nam wychodzi, że nic nie spełnia.

Aga1: ekstremum w punkcie 6, a w 7 punkty przegięcia . Wyszło ze druga pochodna nie ma miejsc zerowych

donde: No tam wyszło że ekstremum jest 1/e i to jest minimum. Coś dalej z tego mam liczyć, czy tyle tylko?

Aga1:

	1
Minimum jest w punkcie		i trzeba obliczyć ile wynosi.
	e

A co z punktami przegięcia, jaki jest warunek konieczny istnienia punktu przegięcia?

Aga1: Zostały dwa punkty do zrobienia, jesteś?

donde: Jestem jestem ciągle, no ale nie wiem teraz zbytnio

donde: (1 / e) * ln(1 / e) = −0.367879441

donde: nie wiem czy dobrze myślę czy źle

donde: No i warunkiem koniecznym aby punkt x0 był punktem przegięcia funkcji jest warunek f''(x0)=0 , o ile druga pochodna w tym punkcie istnieje.

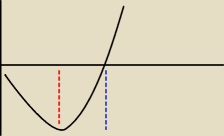
donde: No to rozpisałem sobie tabelkę i narysowałem wg niej wykres i wyszło mi takie coś, gdzie. czerwona kreska pokazuje minimum w 1/e, a niebieska miejsce zerowe w jedynce. I tak funkcja (0,1/e) maleje w 1/e osiąga minimum. (1/e,∞)funkcja rośnie. Funkcja w 1 przecina oś OX (miejsce zerowe) A dlaczego łagodnie maleje i rośnie pokazuje tabelka. x | (0,1/e) | (1/e) | (1/e,1) | (1) | (1,∞) | f(x)' | − | 0 | + | + | + | f(x)''| + | + | + | + | + | Druga pochodna brałem po prostu z przedziałów liczby i podstawiałem pod 1/x i sprawdzałem czy będzie dodatnia czy ujemna. Proszę mój tok myślenia i działania poprawić jakby co.

Aga1: Jeszcze dodam o wypukłości

	1
f"(x)=
	x

1
	>0//*x2
x

1>0 x∊(0,∞) Funkcja jest wypukła na całym przedziale.

donde: Jeszcze mam pytanie na temat punktu: granice w punktach nienależące do dziedziny... Jak coś takiego zrobić..

donde: W każdym razie ślicznie dziękuje za pomoc, to by było na tyle