y=x^2+7x-12
Waretta: y=x
2+7x−12
−podaj postać kanoniczną i iloczynową
−podaj przedziały monotoniczności
−ekstrema, dla jakiego argumentu funkcja przyjmuje ekstremalną wartość i ile ona wynosi
−dla jakich argumentów funkcja przyjmuje NIE dodatnie wartości
−narysuj wykres funkcji
−największą i najmniejszą wartość i przedziale x∊<0;4>
Proszę o PomoC


25 lut 18:15
25 lut 18:16
Waretta: a możesz pomóc w pozostałej części

25 lut 18:24
krystek: ok.Podaj m zerowe i współrzędne wierzchołka − jakie wyliczyłąś
25 lut 18:25
krystek: A dobrze przepisałas funkcje ? x2+7x+12 ?
25 lut 18:27
Waretta: tak,dobrze .. te funkcję pani wymyślała... mam ich 6 w zeszycie i wszystkie mam rozwiązać...
podana jest jedną z nich i właśnie chciałam poprosić o pomoc w rozwiązaniu, aby wzorując się na
tym zrobić pozostałe
obecnie policzyłam postać iloczynową i kanoniczną oraz kiedy funkcja jest rosnąca i malejąca
25 lut 18:31
krystek: ale "brzydka "Δ
25 lut 18:33
Waretta: dalej nie umiem

| | 1 | | 1 | |
p.iloczynowa y=(x+3 |
| −√97)(x+3 |
| +√97) |
| | 2 | | 2 | |
| | 1 | | 1 | |
p.kanoniczna y=(x+3 |
| )2−24 |
| |
| | 2 | | 4 | |
| | 1 | |
funkcja jest malejąca w przedziale (−nieskończoności, −3 |
| ) |
| | 2 | |
| | 1 | |
−−−−−rosnąca−−(−3 |
| ,+nieskończoności) |
| | 2 | |
25 lut 18:36
Waretta: Możecie pomóc?Byłabym dozgonnie wdzięczna

muszę to jakoś rozwiązać, następnie czeka mnie
poprawa sprawdzianu (oczywiście jak już to opanuje) ... ale z moją wiedzą na obecną chwilę
będzie ciężko ...

25 lut 18:40
krystek: x
2+7x+12
Δ=1
a) postać kanoniczna (x+3,5)
2−0,25
iloczynowa (x+4)(x+3)
f↗ dla x∊<−3,5,
∞)
f↘ dla x∊(−
∞, 3,5)
minimum −0,25 dla x=−3,5
25 lut 18:41
krystek: No i dałas radę! Gratuluję.
25 lut 18:42
krystek: wartości niedodatnie ,czyli ujemne i zero dla x∊<x1,x2> dla Twoich obliczeń
25 lut 18:44
Waretta: hmm myślisz, że zmienić ten "−" na "+"
25 lut 18:45
Waretta: hmm.. ale niech już zostanie "−" tak było zapisane,więc nie będę tego zmieniać ...
i jak dalej mam postępować?

25 lut 18:47
krystek:
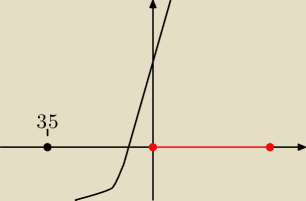
zauważ ,że wierzchołek jest poza przedziałem
f
min=f(0)
f
max=f(4)
25 lut 18:50
Waretta: troszkę nie orientuję się jak to odzwierciedlić na moim przykładzie

25 lut 18:56
krystek:
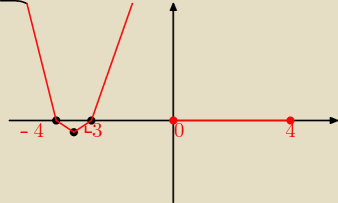
A teraz wykres do moich obliczeń
25 lut 18:59
krystek: m zerowe przybliżone przyjmij √97≈10
25 lut 19:01
Waretta:
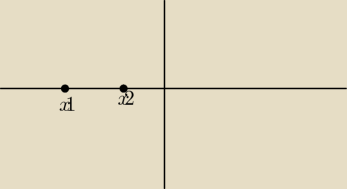
x2=...+
√97
25 lut 19:02
Waretta: napisałam do koleżanki z klasy może tam faktycznie powinien być "+" ... patrząc na moje wyniki
faktycznie są niemiłe

25 lut 19:07
Waretta: a jaką rozgryźć tą ekstremę?
25 lut 19:08
Waretta: jednak powinien być "+".. przepraszam z kłamstewko przez pomyłkę

tak wgl jesteś boski

dzięki za wszystko

25 lut 19:11
krystek: Jaką?
25 lut 19:11
Waretta: ekstrema, dla jakiego argumentu funkcja przyjmuje ekstremalną wartość i ile ona wynosi
25 lut 19:14
krystek: Ekstremum to największa lub najmniejsza wartośc funkcji
Parabola w wierzchołku ma najmniejsza wartość wynosi ona −0,25 jest to wyliczone q
Popatrz na wykres
25 lut 19:17
krystek: godz. 18:41 przeczytaj
25 lut 19:19
Waretta: więc wartość min i max to ekstrema czy "minimum −0,25 dla x=−3,5"
25 lut 19:26
Waretta: byłam ostatnio na korka 3h .. a moja wiedza wciąż jest uboga

25 lut 19:29
Waretta: korkach*
25 lut 19:29
krystek: ok
25 lut 19:30
krystek: Zależy z kim i jak tłumaczy!
25 lut 19:31
Waretta: teraz to już bardzo nikogo odpowiedniego nie znajdę tylko tyle co się "tu" nauczkę
więc jeszcze raz bardzo dziękuje
25 lut 19:34
krystek: To co jeszcze chcesz wiedzieć?
25 lut 19:38
Waretta: a masz może dostępne jakieś materiały .. które rozjaśniły by mój umysł co do funkcji
kwadratowej ...
25 lut 19:38
25 lut 19:39
Waretta: hah trafiłam na "korepetytora online "

25 lut 19:39
krystek: ?
25 lut 19:43
Blazz: x2 + 7x + 12 = < trzeba to skrócić za pomocą wzoru skróconego mnnożenia.. >
8 sty 21:18




 muszę to jakoś rozwiązać, następnie czeka mnie
poprawa sprawdzianu (oczywiście jak już to opanuje) ... ale z moją wiedzą na obecną chwilę
będzie ciężko ...
muszę to jakoś rozwiązać, następnie czeka mnie
poprawa sprawdzianu (oczywiście jak już to opanuje) ... ale z moją wiedzą na obecną chwilę
będzie ciężko ...

 zauważ ,że wierzchołek jest poza przedziałem
fmin=f(0)
fmax=f(4)
zauważ ,że wierzchołek jest poza przedziałem
fmin=f(0)
fmax=f(4)

 A teraz wykres do moich obliczeń
A teraz wykres do moich obliczeń


 tak wgl jesteś boski
tak wgl jesteś boski  dzięki za wszystko
dzięki za wszystko 

