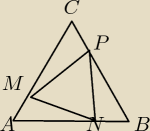
 Trójkąt równoboczny ABC ma bok długości 10cm.Na jego bokach obrano punkty M, N, P tak, że
IAMI=IBNI=ICPI(jak na rysunku.Jak należy wybrać punkty M, N i P, aby pole trójkąta MNP było
najmniejsze?DDDDDD
Trójkąt równoboczny ABC ma bok długości 10cm.Na jego bokach obrano punkty M, N, P tak, że
IAMI=IBNI=ICPI(jak na rysunku.Jak należy wybrać punkty M, N i P, aby pole trójkąta MNP było
najmniejsze?DDDDDD
| 1 | √3 | |||
PANM = | x(10−x)sin60o = | (10x−x2)
| ||
| 2 | 4 |
| √3 | 3√3 | 15√3 | ||||
PMNP = PABC − 3*PANM = 25√3 − 3* | (10x−x2) = | x2 − | x | |||
| 4 | 4 | 2 |
| b | ||
funkcja kwadr. osiąga wartość najmniejszą w wierzchołku, czyli xw = − | = 5
| |
| 2a |

 oczywiście rozwiązanie wymaga "dopieszczenia" − np. wspomnienia, że trójkąty AMN, BNP i CPM są
przystające
oczywiście rozwiązanie wymaga "dopieszczenia" − np. wspomnienia, że trójkąty AMN, BNP i CPM są
przystające
