Wytłumaczył by mi ktoś to zadanie? Bardzo proszę. Janet: Wytłumaczył by mi ktoś to zadanie? Bardzo proszę. Kwadrat o boku ABCDjest wpisany w okrąg o promieniu R. Wykaż, że dla dowolnego punktu M leżącego na tym okręgu spełniona jest równość: |MA|² + |MB|² + |MC|² + |MD|² = 8R²

ejendi: MA²+MB²=a² czyli cała suma to 2a² R=a/2 8R²=8a²/4=2a²

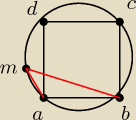
Janet: skąd wiemy, że |MA| ² + |MB|² = a² ?

ICSP: Rozpatrzmy : |MD|² + |MB|² = |BD|² zauważmy że odcinek |BD| jest średnicą ⇒ Δ_MBD jest prostokątny. |MB|² + |MD|² = (2R)² analogicznie możemy dowieść że: |MC|² + |MA|² = (2R)² sumujemy obustronnie równania : |MB|² + |MD|² + |MC|² + |MA|² = (2R)² + (2R²) c.n.u.

ICSP: ... = (2R)² + (2R)² mały błąd

Janet: dziękuję ICSP , a pomógłbyś mi jeszcze z 2 zadaniami? bo ich nie rozumiem. W czworokącie ABCD wpisanym w okrąg o długości łuku odpowiadającym cięciwom AB, BC, CD są równe. wykaż, że czworokąt ABCD jest trapezem. chodzi o to aby pokazać,że np odcinki AB i CD są do siebie równoległe? czy źle myślę?

ICSP: dobrze myślisz

ICSP: Ja teraz wyruszam na mistrzostwa świata Może będę później

Janet: ok, będę wdzięczna jak tu jeszcze zajrzysz jak wrócisz

Janet: pomoże mi ktoś to wykazać , bo nie radzę sobie z tym ?

Janet: może być coś takiego? że skoro |AB| I |CD| są równe x to prosta przechodząca przez punkty A i D i prosta przechodząca przez punkty B i C są równoległe, bo odległość między nimi jest taka sama?