 S=3:4 oraz
BC=12.Znajdz dł odcinka BS
3.Przekatne trapezu AC oraz BD przecinaja sie punkcie S.Znajdz dł obu przekatnych wiedzac ze
AB=12,CD=8,AS=6 oraz BS=3
4.Przekatne trapezu przecinaja sie w punkcie S.PolePole trojkata ABS wynosi P1=36,a pole
trojkata BCS P2=9.Znajdz pole trapezu
5.W trapezie rownoramiennym ABCD kat BAD=60,a odległosc srodka okregu wpisanego od wierzchołka
A rowna jest OA=2.Znajdz boki trapezu
6.W trapezie rownoramiennym dane sa podstawy AB=10,CD=2.Znajdz ramiona trapezu wiedzac ze w
trapezie mozna opisac okrag.
7Dane jest pole rombu P=2pierwiastki z 3 oraz kast ostry alfa=60.Znajdz promien okregu
wpisanego
8/Dłuzsza przekatna rombu rowna jest AC=10, a kat ostry 60.Znajdz promien okragu wpisanego
9.W trapezie rownoramiennym ABCD kat ADC=120,a odległosc srodka okregu wpisanego od wierzchołka
D rowna jest OD=2 pierwiastki z 3.Znajdz boki trapezu
10.W czworokacie ABCD kat alfa=50,beta=100.Znajdz pozostałe kąty wiedzac ze na czworokacie tym
mozna opisac okrag.
11.Znajdz promien okragu opisanego na prostokacie o bokach AB=20 oraz AD=10
12.Dane sa podstawy trapezu AB=20,CD=12.Znajdz ramiona trapezu wiedzac ze srodek okregu
opisanego na tym trapezie lezy na dłuzszej podstawie
13.Podstawy trapezu rownoramiennego ABCD wynosza AB=16 oraz CD=12, a wys DK=14.Znajdz promien
okregu opisanego
S=3:4 oraz
BC=12.Znajdz dł odcinka BS
3.Przekatne trapezu AC oraz BD przecinaja sie punkcie S.Znajdz dł obu przekatnych wiedzac ze
AB=12,CD=8,AS=6 oraz BS=3
4.Przekatne trapezu przecinaja sie w punkcie S.PolePole trojkata ABS wynosi P1=36,a pole
trojkata BCS P2=9.Znajdz pole trapezu
5.W trapezie rownoramiennym ABCD kat BAD=60,a odległosc srodka okregu wpisanego od wierzchołka
A rowna jest OA=2.Znajdz boki trapezu
6.W trapezie rownoramiennym dane sa podstawy AB=10,CD=2.Znajdz ramiona trapezu wiedzac ze w
trapezie mozna opisac okrag.
7Dane jest pole rombu P=2pierwiastki z 3 oraz kast ostry alfa=60.Znajdz promien okregu
wpisanego
8/Dłuzsza przekatna rombu rowna jest AC=10, a kat ostry 60.Znajdz promien okragu wpisanego
9.W trapezie rownoramiennym ABCD kat ADC=120,a odległosc srodka okregu wpisanego od wierzchołka
D rowna jest OD=2 pierwiastki z 3.Znajdz boki trapezu
10.W czworokacie ABCD kat alfa=50,beta=100.Znajdz pozostałe kąty wiedzac ze na czworokacie tym
mozna opisac okrag.
11.Znajdz promien okragu opisanego na prostokacie o bokach AB=20 oraz AD=10
12.Dane sa podstawy trapezu AB=20,CD=12.Znajdz ramiona trapezu wiedzac ze srodek okregu
opisanego na tym trapezie lezy na dłuzszej podstawie
13.Podstawy trapezu rownoramiennego ABCD wynosza AB=16 oraz CD=12, a wys DK=14.Znajdz promien
okregu opisanego
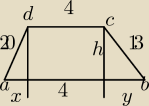 x+y = 21
400= x2 +h2
169 = y2 + h2
400−169 = x2 − y2
231= x2 − y2
231 = (21−y)2 − y2
231= 441 − 42y
210 = 42y
y=5
x=16
169= 25+h2
h= 12
d1= √400+144
d2= √81+144
x+y = 21
400= x2 +h2
169 = y2 + h2
400−169 = x2 − y2
231= x2 − y2
231 = (21−y)2 − y2
231= 441 − 42y
210 = 42y
y=5
x=16
169= 25+h2
h= 12
d1= √400+144
d2= √81+144
 d1 = √400 + 144 = √544 = √16 * 34 = 4√34
d2 = √81 + 144 = √225 = 15
d1 = √400 + 144 = √544 = √16 * 34 = 4√34
d2 = √81 + 144 = √225 = 15
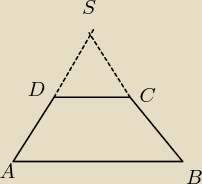 Zad2
Zad2
| |AD| | 3 | ||
= | |||
| |DS| | 4 |
| AD | BC | ||
= | |||
| DS | SC |
| 3 | 12 | ||
= | |||
| 4 | |SC| |
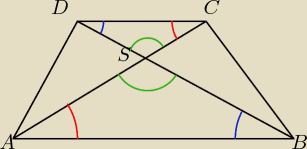 Zad3
ΔABS ≈ ΔDSC z cechy KKK
mamy dane :
|AB| oraz |DC|
możemy więc obliczyć skalę podobieństwa tych trójkątów :
Zad3
ΔABS ≈ ΔDSC z cechy KKK
mamy dane :
|AB| oraz |DC|
możemy więc obliczyć skalę podobieństwa tych trójkątów :
| |AB| | 12 | 3 | ||||
k = | = | = | ||||
| |CD| | 8 | 2 |
| |AS| | |BS| | |||
k = | = | |||
| |SC| | |SD| |
| 3 | |
= U{6}{|SC| | |
| 2 |
| |BS| | ||
k = | ||
| |SD| |
| 3 | |
= U{3}{|SD| | |
| 2 |
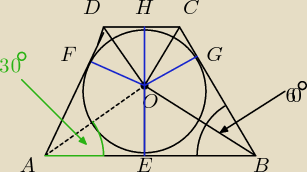 Zad5
Niebieskie odcinki mają równą długość . Ponadto:
|AE| = |EB| = |BG| = |AF|
Zad5
Niebieskie odcinki mają równą długość . Ponadto:
|AE| = |EB| = |BG| = |AF|
| AE | |
= cos0o ⇒ AE = √3 | |
| AO |
| r | |
= sin30o | |
| |AO| |
| r | |
= tg60o | |
| DF |
| r | √3 | |||
|DF| = | = | |||
| tg60o | 3 |
| √3 | ||
|AD| = |BC| = √3 + | ||
| 3 |
| 2√3 | ||
|DC| = | ||
| 3 |


 Łatwe dowody
Łatwe dowody 