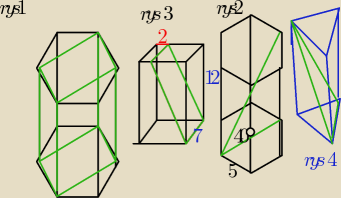
Graniastosłupy Marta: Prosze bardzo o rozwiązanie lub o podanie wskazówek jak mam rozwiązać podane zadania Zad.1 Z graniastosłupa prawidłowego sześciokatnego wycięto prostopadłościan. Jaki procent objetości graniastosłupa stanowi objętość prostopadłoscianu.(rys. wyżej) prosze o obliczenia a) 50% b) około 55% c) około 67% d) 75% Zad.2 Jaka jest długość przekątnej graniastosłupa prawidłowego sześciokatnego , zaznaczonej na rysynku wyżej (rys2) proszę o obliczenia a) ok.13 b) ok. 12 c) 8 d) 7 Zad.3 W graniastosłupie prawidłowym sześciokątnym wszystkie krawedzie mają długość 10. Krotszaprzekatna tego graniastosłupa ma długość? Proszę obliczyć a) 10√3cm b) 10√5cm c) 20cm d) 21√3cm Zad.4 Graniastosłup prawidłowy dziesięciokatny ma wysokość 3cm. Okrąg opisany n ajego podstawie ma promień 3cm. Najdłuzsza przekatna tego graniastosłupa ma długosć: (prosze obliczyc) a) 3 cm b) 3√2 cm c) 3√5 cm d) 9cm Zad.5 kąt α miedzy przekatna sześcinu a jego krawędzią spełnia warunek (proszę obliczyć, wyjaśnić) a) tgα=¹_√3 b) sinα=√²₃ c) ctgα=√2 d) cosα=¹_√2 Zad.6 Graniastosłup trójkątny o krawędzi podstawy 2 i objętości 3 ma pole powierzni całkowitej rowne (obliczyć) a) 12 b) 8√3 c) 16 d) 18√3 Zad.7 Podstawą pewnego graniastoslupa prostego jest rownoległobok o bokach 5cm i 8cm Kąt ostry między ścianami ma miarę 30^o Pole podstawy tego graniastosłupa wynosi (obliczyc) a) 20o{3}cm³ b) 40 cm³ c) 10√3cm³ d) 20 cm ³ Zad.8 Wszystkie krawędzie graniastosłupa prawidłowego sześciokatnego mają taką samą długość. Pod jakim kątem nachylona jest podstawa graniostosłupa dłuższa z jego przekatnych? (obluczyc) a) ok27^o b) ok. 63^o c)30^o d) 60^o Zad.9 Jakie pole ma zaznaczony na rysunku przekrój graniastosłupa prawidłowego czworokatnego? (oboiczyć) rys 3 a)91 b)84 c)60 d) 35 Zad. 10 Na rysunku wyżej (rys4)przedstawiono przekrój graniostosłupa prawidłowego trójkątnego. Krawedz podstawy tego graniastosłupa wynosi 4 a plaszczyzna przekroju nachylona jest do płaszczyzny podstawy pod kątem 60^o Pole tego przekroju wynosi (obliczyc) a) 4√3 b) ^8√3₃ c) 8√3 d) ⁶_√3

ejendi: 1) ∡w=180−360/2=120 b−bok, reszta boków=a Pp=ab b=2asin60=a√3 Pp=a²√3 P=n/4*ctg180/n=1,5a²*√3

	1
Pp/P=		=0,666666667
	1,5

ejendi: 9) P=√(7−2)²+12²*7

ejendi: a−bok pp przek, podst. ps przek sześć pp=a*√2 a/pp=sin(90−α)=√2/2=cosα