?? matma: Ostrosłup prawidłowy czworokątny przecięto płaszczyzną przechodzącą przez wierzchołek ostrosłupa i przekątna podstawy. Przekrój ten jest trójkątem równobocznym o polu S =9√3 . Oblicz kąt nachylenia ściany bocznej do płaszczyzny podst w tym ostrosłupie(wynik zaokrąglij do pełnych stopni)

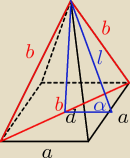
Artur z miasta Neptuna: b = d d = a√2

	b2√3
PΔ = 9√3 =		⇔ b=3*2 = 6
	4

b=6 ⇔ a = 3√2

	a		126		√126
l2 = b2 − (		)2 = 36 − 18/4 =		⇔ l =
	2		4		2

	a		3√2 * 2		6√2		2√7
cos α =		=		=		=		≈ 0.756
	l		√126		3√2√7		7

Artur z miasta Neptuna: i sięgasz do tablic

matma: a skąd b² w drugiej linijce od spodu ?

Aga1: Wysokość ostrosłupa= wysokości trójkąta równobocznego o boku b.

	b√3
h=
	2

	1
l2=(		a)2+h2
	2

	0,5a
cosα=
	l