pole powierzchni
aniaa :): Oblicz pole powierzchni:
a) graniastosłupa prawidłowego trójkątnego o krawędzi podstawy √3 i wysokości 2
b) graniastosłupa prawidłowego czworokątnego o wysokości 4 i przekątnej długości 5
22 lut 20:04
dero2005:
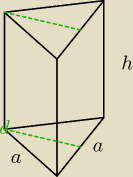
zad a)
a =
√3
h = 2
liczymy pole podstawy P
p
| | a2√3 | | (√3)2*√3 | | 3 | |
Pp = |
| = |
| = |
| √3
|
| | 4 | | 4 | | 4 | |
liczymy pole pow bocznej P
b
P
b = 3*a*h = 3*
√3*2 = 6
√3
liczymy pole pow całkowitej P
c
| | 3 | | 15 | |
Pc = 2*Pp + Pb = 2* |
| √3 + 6√3 = |
| √3
|
| | 4 | | 2 | |
22 lut 21:34
Monika:
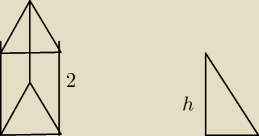
a)
h
2 + (1/2
√3)
2 = (
√3)
2 − z tw Pitagorasa liczymy wysokość a potem Pole podstawy i pole
boczne
h = 3/2
Pp = 1/2 a *h = 1/2 P{3} * 3/2 = # P{3}/4
Pb = a*h = 2 P{3}
Pc = 2Pp + 3Pb = 6
√3 + 3
√3 / 2
b)
tu najpierw liczymy przekątną podstawy d z tw. Pitagorasa (wyjdzie 3)
a potem krawędź podstawy a
22 lut 21:40
dero2005:
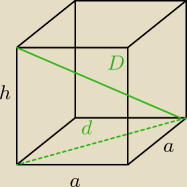
h = 4
D = 5
d =
√D2 − h2 =
√52 − 42 =
√25−16 =
√9 = 3
| | 9 | |
Pc = 2*Pp + Pb = 2* |
| + 18 = 27 |
| | 2 | |
22 lut 21:45
joł jołaj: dero:
Pp = 2 * a2
Pb = 4 * ah
Pc = Pp * Pb
Pole calkowite = Pola podstawy + Pola boczne
a z twojego liczenia wychodzi:
Pole calkowite = dwa pola podstawy + pola boczne
z tego co mi nauczycielka mowila, taki zapis jest nie prawidlowy, ale wynik jest dobry
22 lut 21:54
joł jołaj: rozumiesz? o to chodzi, ze w Pc juz nie mozna mnozyc, trzeba to zrobic w obilczaniu pol
22 lut 21:56
dero2005:
podstawa to jest to co jest na dole, to co na górze to nadstawa
Pc = 2Pp+Pc a nie Pp*Pb
22 lut 22:00
 zad a)
a = √3
h = 2
liczymy pole podstawy Pp
zad a)
a = √3
h = 2
liczymy pole podstawy Pp
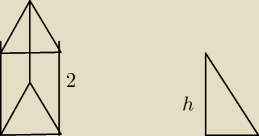 a)
h2 + (1/2 √3)2 = (√3)2 − z tw Pitagorasa liczymy wysokość a potem Pole podstawy i pole
boczne
h = 3/2
Pp = 1/2 a *h = 1/2 P{3} * 3/2 = # P{3}/4
Pb = a*h = 2 P{3}
Pc = 2Pp + 3Pb = 6 √3 + 3 √3 / 2
b)
tu najpierw liczymy przekątną podstawy d z tw. Pitagorasa (wyjdzie 3)
a potem krawędź podstawy a
a)
h2 + (1/2 √3)2 = (√3)2 − z tw Pitagorasa liczymy wysokość a potem Pole podstawy i pole
boczne
h = 3/2
Pp = 1/2 a *h = 1/2 P{3} * 3/2 = # P{3}/4
Pb = a*h = 2 P{3}
Pc = 2Pp + 3Pb = 6 √3 + 3 √3 / 2
b)
tu najpierw liczymy przekątną podstawy d z tw. Pitagorasa (wyjdzie 3)
a potem krawędź podstawy a
 h = 4
D = 5
d = √D2 − h2 = √52 − 42 = √25−16 = √9 = 3
h = 4
D = 5
d = √D2 − h2 = √52 − 42 = √25−16 = √9 = 3