RÓWNANIE PROSTEJ Maciek2: spotkałem się z dotąd nie znanym mi wzorem na równanie równoległej do prostej w postaci ogólnej Ax+By+C=0 Mianowicie prostopadłą do danej prostej opisuje się jako −Bx+Ay+C₁=0 Spotkaliście się juz z takim równaniem?

krystek:

	−A		C		B
y=		x−		prostopadła a2=
	B		B		A

	B
y=		x+b
	A

Ay−Bx+C₁=

Man in black: Wiesz jaka jest interpretacja A i B w równaniu prostej Ax+By+C=0? Warto znać takie rzeczy.

krystek: Wiem , wiem !

pigor: ... no właśnie , piękna rzecz, są to współrzędne wektora [A,B] prostopadłego (normalnego) do prostej danej takim równaniem, na studiach jak znalazł , bo równanie analogiczne Ax+By+Cz+D=0 to równanie płaszczyzny , a [A,B,C] to wektor prostopadły do niej i może starczy . ...)

krystek: Ale w szkole średniej −obecnie− wektory nie sa omawiane −podaje się gotowce −nie wyjaśnia .

Basiek: E tam, my w tym roku właśnie omawialiśmy zależność prostej od wektora. Na tę okoliczność robiliśmy nawet jakieś zadania. Chociaż szczerze przyznam, że niewiele zapamiętałam.

Maciek2: @Man in Black no wiesz....nie wiem o którą ci dokładnie chodzi xD

krystek: @Basiek rachunek wektorowy jest "lizany" stąd wiedza "umyka"

Basiek: @ Krystek Powiedziałabym, że "paruje z całej objętości mózgu" Muszę sobie to przerobić jakoś przed maturą, ale szczerze mówiąc, nigdzie nie ma tego zebranego w formie, która byłaby w całości przydatna i do tego przejrzysta; a szkoda.

Maciek2: co w ogóle jest wymagane na maturze z wektorów?

Basiek: Podstawa/ rozszerzenie?

krystek: Długość wektora , współrzędne.

krystek: Podział na połowy− współrzędne środka , podział w danym stosunku.

Maciek2: na podstawie nie ma wektorów

Basiek: Tak mi się właśnie wydawało. Na rozszerzeniu... w sumie też niewiele. Tzn. niby sporo czasem ułatwiają, ale wydaje mi się, że nie są niezbędne.... . Chyba. A przynajmniej ja się z takim zadaniem nie spotkałam.

krystek: A zadania z równoległobokami?

Basiek: http://panmarek.sasiedzi.pl/ZESTAWIENIE/GEOMETRIA%20ANALITYCZNA/001-Rownanie%20prostej%20na%20plaszczyznie.htm Tu temat jest trochę "dziubnięty"

Basiek: No hm.... to prostymi da się zrobić, nie trzeba do tego wektorów (?)

krystek: A wektorami szybciej −równośc wektorów .

Basiek: Hm, jak już wspomniałeś Krystek − rachunek wektorowy jest "lizany", więc czasem lepiej iść dłuższą ścieżką, ale pewniejszą

krystek: @Basie tam nie jest "dziubnięty"− wyjaśnione w oparciu o rachunek wektorowy. Na studiach opanujesz.

krystek: Oczywiście ,zgadzam się !

Eta: i

Basiek: Hm, skupiłam się tylko na "Równanie normalne prostej. ", ale fakt; analityczna jest tam w dość szerokim zakresie opisana.

krystek:

Maciek2: dzięki Basiek

Basiek: Nie ma problemu mnie też się zapewne przyda

Mila: Oto proste pisanie równań równoległych i prostopadłych. Konkret: k: 2x−y +5 =0 l: 2x−y +C=0 to są wszystkie równoległe do pierwszej. C wyznaczamy mając wsp. punktu przez który prosta l ma przechodzić. m: 2x−y +5 =0 dana prosta n: x+2y+C =0 są wszystkie prostopadłe do m. C wyznaczamy mając wsp. punktu przez który prosta n ma przechodzić.

Basiek: Mila, czy gdyby k: 2x−y+5=0 l: 4x−2y+C=0 też byłyby równoległe? Coś mi tak świta...

Mila: Też, ale konkretną prostą otrzymasz, gdy poprowadzisz ją przez podany punkt.( jednoznacznie wyznaczysz C) Zrób konkretny przykład (może być taki, który robiłaś z rownania kierunkowego) to Ci sprawdzę.

Basiek: W zasadzie, ja tylko przypięłam się do tematu i przypomniałam sobie pewne przydatne informacje, nie mam żadnego konkretu na tę okazję. Aczkolwiek dziękuję Mila

Mila: Każdy musi sam znaleźć swoją ścieżkę do wiedzy.

Basiek: Moja jest coś... zawiła i... muszę zacząć się uczyć (od jutra).

pigor: .... oczywiście tak , bo wektory [2,−1] i [4,−2]=2[2−1] normalne tych prostych są równoległe (różnią się tylko długością) . ...

Basiek: Czyli do prostej: k: 2x−y+5=0 równoległy jest wektor [2,−1], a prostopadły?

ejendi: Ax+By+C=0 (A,B) to jest wektor a wektor ⊥do(A,B) będzie (B,−A) albo (−B,A)

Basiek: a wektor ⊥do(A,B) będzie (B,−A) albo (−B,A) − bez różnicy? Oba będą prostopadłe?... Jej... trochę ciężko mi sobie to... uświadomić i wbić do głowy. Ale postaram się. Dziękuję

Basiek: O, a taki wektor (−A,−B) ? Ma jakieś "specjalne" właściwości odnośnie prostej?

Basiek: Hm, w sumie..... to będzie jedynie wektor przeciwny do (A,B)− tak? Czyli też będzie równoległy?

Mila: Najlepiej narysuj te wektorki w układzie wsp. . Pięknie widać wszystko.

Basiek: Narysowanie wektora w układzie współrzędnych stanowi pewien... problem.

Bartek0807: wektor v=[a,b] gdzie a jest początkiem (zaczepieniem) a "b" końcem. Albo inaczej ...gdzie tkwi problem?

Basiek: No... więc, jak tak myślę ogólnie i nie mam żadnego konkrety, to mam taki problem, że nie umiem tego narysować. Może hm... rozważę jakiś przykład, np.: v=[2,3] to będzie.... no, jak to narysować? Czy np [5−3,7−4]=v, więc.... np. wektor będzie wyznaczać odcinek między A(5,7) B(3,4) ? O.o

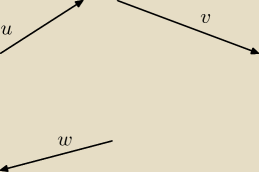
Mila: u=[3,2] v−[5,−2] w=[−3,−1]

Mila: Niestety nie wyszły kratki. wektor u −3 kratki w prawo, dwie do góry.

Basiek: Hm, rozumiem. Więc... te współrzędne to zwyczajnie są długości [góra−dół, prawo−lewo], powoli chyba zaczynam budować sobie właściwy obraz wektorów w głowie.

Basiek: * [prawo−lewo,góra−dół] , bo pierwsza współrzędna jest przecież uzależniona od x−a. Okej. Przepraszam, że jestem taka problematyczna.

Bartek0807: pomyśl sobie o wektorze jako o przesunięciu np v=[2,3] przeszuwasz wektor w prawo o dwa i o 3 w góre. Zapoznaj się też z translacją wektora, wtedy wektory nie będą tajemnicą

Mila: góra + dół− w prawo+ w lewo − Chodzisz jak robot, pod kątem prostym.

Basiek: Paradoksalnie translacje i przekształcenia wykresów ogarniam. Okej, okej... chyba muszę się przespać z tym problemem. Dziękuję, jak coś jeszcze sobie ubzduram w tej sprawie− to się odezwę.

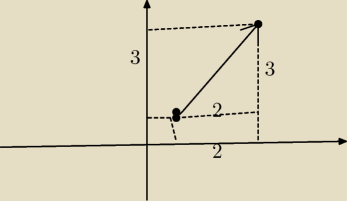
krystek: Krótko: wektor[2,3] rysujesz prostokąt o tych wymiwrach i przekątna z lewego dolnego rogu jest tym wektorem. Czyli jego rzut na oś Ox da odc 2 a na oś OY da 3. I takich wektorów możesz narysowac wiele.

Basiek: I stąd wzór na długość wektora, którego ostatnio nie pamiętałam ...

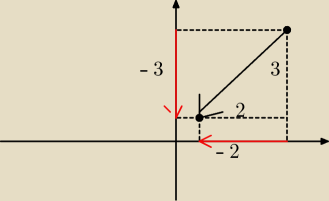
krystek: wektor [−2,3]− przekątna prostokąta z prawego dolnego wierzchołka jest tym wektorem.

Bartek0807: i jeszcze jedna sprawa o której pewnie wiesz : jeżeli przesuwamy funkcje y=f(x) o wektor [2,3] to powstaje taki oto wzor funkcji y−3=f(x−2) ⇔ y=f(x−2) +3 z definicji o odległości punktów na osi liczbowej

Basiek: O dziwo, rozumiem zwroty.... i hm. Teraz już nawet doszłam do konstruktywnego wniosku, że wektory [A,B] i [−A,−B] są równoległe

Basiek: "z definicji o odległości punktów na osi liczbowej" −> do tego momentu rozumiałam

krystek:

krystek:

Basiek: Rozumiem, dziękuję Krystek

Mila: Sympatyczna dyskusja, co Maciek na to?

krystek: IWszystko jasne? i teraz masz współrzędne wektora [a_x, a_y] gdze a_x=x_B−x_A a_y=y_b−y_A stąd [x_A−x_B, y_B−y_A] i liczysz długośc wektora z Pitagorasa.

Basiek: Mhm. Póki co jasne, czasem mnie po kilku dniach dopiero nachodzą niepokojące pytania. Na tę chwilę− rozumiem. W sumie cieszy mnie to, bo samą analityczną bardzo lubię, w sumie to mój ulubiony temat, więc troszkę mi brakowało w niektórych zadaniach wektorów. A Maciek chyba zwiał Może sobie to w najbliższym czasie przyswoi, bo wydawał się zainteresowany tematem, a ja chyba skorzystałam najwięcej Dziękuję wszystkim jeszcze raz

krystek: Cały problem w tym,że "liżesię " a nie uczy!

Maciek2: Maciek już zrozumiał zerknołem do podręcznika i nad nim siedziałem ale i tak pewnie będę to rozkminiał pod róznymi kątami

Basiek: Ja zgubiłam podręcznik, jeśli mam być szczera. Ale i tak nigdy go nie lubiłam

Maciek2: wpadłem jeszcze na takie coś: wektory są prostopadłe wtedy i tylko wtedy, gdy ich iloczyn skalarny wynosi zero, czyli ux vx + uv vy = 0 szkoda tylko że w mojej szkole o skalarach pewnie nigdy nie słyszeli

krystek: zerknąłem

Basiek: Dobra, koniec. Zasiedziałam się przez te wektory i już mi się nawet nie chce przez nie spać. Ale i tak trzeba. Dziękuję jeszcze raz baaaardzo za masę cierpliwości w stosunku do mnie i taką życzliwość. Dobranoc!

krystek: Śpij spokojnie!

krystek: @Maciek ponieważ cos90=0 a jest to kąt między wektorami!

Maciek2: @krystek wiem czemu, wiem też że jeśli wynik jest 0< to jest to kąt rozwary a gdy 0> to ostry. Chodziło mi o to że takie fascynujące rzeczy poznam bliżej dopiero na studiach

krystek: Więc nie mów ,że w szkole o tym nie słyszeli! Tego nie uczyli ,ponieważ wyrzucono to z programu, jak i pochodne!

krystek: @Maciek teraz widzę ,że Ty napisałeś ten post− i Ty jesteś na studiach i o to pytałeś?

Maciek2: krystek spokojnie nie obrzucam ich błotem. Nie krzycz na mnie. Wyraziłem tylko zartem moje zaciekawienie i chęć eksporacji matematyki. Mój kolega miał skalary u siebie ...tak wiem że chodzi tu tylko o troskę nauczyciela by zaspokajać młode umysły i być może o czas więc im wybaczam tak jak i wybaczam sobie i krystek przebacz też mi. Dziękuję wszystkim za czas i za wiedzę przekazaną Dobranoc

Maciek2: krystek, krystek.....czytanie ze zrozumieniem...."Chodziło mi o to że takie fascynujące rzeczy poznam bliżej dopiero na studiach "

krystek: @Maciek a kto mówi o krzyku !

Maciek2: nie wiem...wykrzyknik mi tak troszeczkę zasugerował...nie powiem że nie.

krystek: Co tutaj fascynującego − po prostu wiedza! n−ty wymiar −to dopiero fascynacja!

Maciek2: czarna dziura, kwanty, wymiary to dopiero fascynacja widzisz ciebie może fascynować teoria a mnie matematyka stosowana, choć nie powiem że dumanie nad największymi problemami dawnych czasów może mieć swój klimat

krystek: @Maciek opanuj podstawową wiedzę! Dobrego samopoczucia i dobrej nocy życzę!

Maciek2: ktoś tu chyba ma gorszy dzień nie lubie kiedy ktoś zachowuje się ponad mnie kiedy powinien zakładać chociaż że jestem jeszcze młody i mam prawo do niewiedzy. Wyżyłeś się na młodszym brawo cywilizacja jest dumna.

krystek: ?