Funkcja Izaura:

	−2 √(x2 − 9) 2
f(x) =
	(x − 3) (x + 3)

a) Podaj dziedzinę i zbiór wartości funkcji. D=R − {−3; 3}

	1
b) Wyznacz zbiór rozwiązań dla nierówności f(x) ≥
	2

tn: dziedzinę dobrze wyznaczyłaś. zostaje Ci nierówność, z tym, ze na czym polega Twój problem z tym zadaniem?

tn: po prostu rozwiąż ją, pomnóż stronami przez mianownik, potem uwaga bo będzie wartość bezwzględna; −4|x²−9|≥x²−9 dokończyć to

Izaura: a zbiór wartości? bo własciwie z tym mam problem

Izaura: bop w nierównościach mnozymi jako kwadrat mianownika i nierówność wychodzi −4|(x² − 9)| ≥ (x² −9) ² i wtedy parametr t = x² − 9 ... to wiem... ale ten zbiór wartości mnie zastanawia jak się to wyznaczało ?

Izaura: oraz założenie że t ≥ 0 czyli t² + 4 t ≤ 0 t (t + 4) ≤ 0

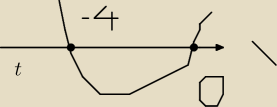
Izaura: potem t ∊ <−4; 0> część wspólna z założeniem że t ≥ 0 daje nam t = 0 i mamy x² = 9 czyli x =−3 i x = 3 ... a to jest bez sensu bo to nie nalezy do dziedziny... wiec sprzeczność... chyba że źle to rozumuję

Izaura: nie przepraszam mamy −4 t² ≥ t²

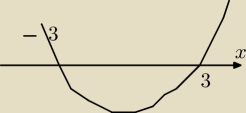
Izaura: 5 t² ≤ 0 /:5 t² ≤ 0 x² − 9 ≤ 0 x ∊ (−3; 3).... ok... a ten zbiór wartości ?

Izaura: pomijając fakt, że t² nie może byc mniejsze od zera.... co najwyżej jemu równe.... ale spoko.... bo wtedy i tak x by znów wyszedł poza dziedziną... ehhh...

Izaura: rozwiązanie że x ∊ (−3; 3) jest spoko.... ponawiam pytanie: jak obliczyć zbiór wartości?