Help!!!
kasiaaa:
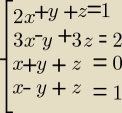
treść :
Na podstawie twierdzenia Kroneckera− Capellego podaj ilość rozwiązań układu równań, na wstępie
wyznacz te rozwiązania (jeżeli istnieją) stosując metodę eliminacji Gaussa.
22 lut 13:40
kasiaaa: pomoże ktoś?
23 lut 11:24
Artur z miasta Neptuna:
wyznaczyłaś z tw. Kroneckera− Capellego ilość rozwiązań ? Nie ? to przypomnij sobie (i nam) to
twierdzenie.
eliminacja Gaussa polega na takim dodawaniu/odejmowaniu/przemnażaniu kolejnych równań (wierszy
macierzy), aby uzyskać 'górnotrójkątną' (same zera poniżej głównej przekątnej) −−− z takiej
pozycji łatwo wyznaczyć rozwiązania układu (poczynając od dołu i biegnąć ku górze).
Ewentualnie metodę eliminacji Gaussa można prowadzi się aż do uzyskania macierzy diagonalnej (a
niektórzy karzą nawet do jednostkowej) − to wszystko zależy od prowadzącego.
23 lut 11:59
Artur z miasta Neptuna:
Jeśli już lecimy metodą Gaussa to:
1. W3 zamień miejscami z W1 ... tak samo W2 z W4.
2. nowe W2 − nowe W1 ; nowe W3 − 2* nowe W1 ; nowe W4 − 3* nowe W1 /// masz już
pierwsze trzy zera
3. W2/2
4. W3 − W2 ; W4 − 4W2
5. W4 − 'ileś tam'W3
i już skończyłaś metodę eliminacji Gaussa.
wypisujesz równania i wyznaczasz rozwiązania
23 lut 12:05
kasiaaa: no tak ale my nigdy na ćwiczeniach nie robiliśmy takiego równania zawsze z3 równaniami a nie z
4 a on tu daje takie a 3 bym wiedziała o co chodzi bo z 4 to pewnie inaczej sie robi ?czy tak
samo?
23 lut 13:01
Man in black: Identycznie z 2, 3, 4, 5 itd...
23 lut 13:02
Artur z miasta Neptuna:
niee ... tak samo ... tylko ten [czwarty] się "wyzeruje" ... jeżeli się nie wyzeruje to
wyjdzie, sprzeczne (np. 0 = 1)
23 lut 13:05
Man in black: Musisz utworzyć macierz współczynników A i macierz uzupełnioną U; następnie liczysz rząd A i
rząd U. Układ ten ma rozwiązanie tylko wtedy, gdy te rzędy są równe. Jeżeli te równe rzędy są
równe liczbie niewiadomych (u Ciebie to 4) to masz jedno rozwiązanie. W przeciwnym przypadku
masz nieskończenie wiele rozwiązań zależnych od kilku parametrów (u Ciebie od 4 − rząd A).
To jest właśnie tw. Kroneckera−Capellego.
23 lut 13:05
30 maj 01:32
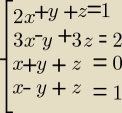 treść :
Na podstawie twierdzenia Kroneckera− Capellego podaj ilość rozwiązań układu równań, na wstępie
wyznacz te rozwiązania (jeżeli istnieją) stosując metodę eliminacji Gaussa.
treść :
Na podstawie twierdzenia Kroneckera− Capellego podaj ilość rozwiązań układu równań, na wstępie
wyznacz te rozwiązania (jeżeli istnieją) stosując metodę eliminacji Gaussa.