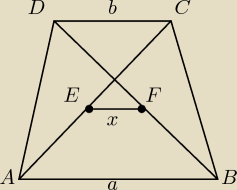
 Ktoś pomoże mi udowodnić wektorowo twierdzenie, że odcinek łączący środki przekątnych w
trapezie jest równoległy do podstaw, a jego długość x jest równa (a−b)/2.
Ktoś pomoże mi udowodnić wektorowo twierdzenie, że odcinek łączący środki przekątnych w
trapezie jest równoległy do podstaw, a jego długość x jest równa (a−b)/2.
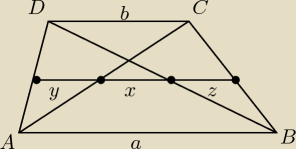 1.(a+b)/2=x+y+z tw. o srodkowej trapezu
zΔABD:
2.x+y=a/2; y=a/2−x tw. Talesa
zΔABC:
3.x+z=a/2; z=a/2−x
2 i 3 do 1
a/2+b/2=x+a/2−x+a/2−x
x=a−a/2−b/2
1.(a+b)/2=x+y+z tw. o srodkowej trapezu
zΔABD:
2.x+y=a/2; y=a/2−x tw. Talesa
zΔABC:
3.x+z=a/2; z=a/2−x
2 i 3 do 1
a/2+b/2=x+a/2−x+a/2−x
x=a−a/2−b/2
| a−b | ||
x= | ||
| 2 |