 Ściana boczna ostrosłupa prawidłowego sześciokątnego jest nachylona do płaszczyzny podstawy pod
katem 30 stopni, a jej wysokość jest równa 3√3.Oblicz objętość tego ostrosłupa.
Ściana boczna ostrosłupa prawidłowego sześciokątnego jest nachylona do płaszczyzny podstawy pod
katem 30 stopni, a jej wysokość jest równa 3√3.Oblicz objętość tego ostrosłupa.
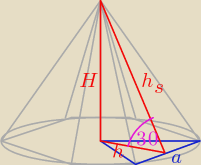 hs = 3√3
hs = 3√3
| h | √3 | ||
= cos 30o = | |||
| 3√3 | 2 |
| 9 | ||
h = | ||
| 2 |
| 2 | 2 | 9 | ||||
a = | √3h = | √3* | = 3√3
| |||
| 3 | 3 | 2 |
| 3a2√3 | 81√3 | |||
Pp = | = | |||
| 2 | 2 |
| H | |
= sin30o = 12
| |
| hs |
| 3√3 | ||
H = | ||
| 2 |
| Pp*H | ||
V = | = −−− dokończ | |
| 3 |