Trójkąt Zygmuś: W trójkąt o bokach a=8,b=6,c=4 wpisano okrąg.Oblicz odległości środka tego okręgu wpisanego od wierzchołków tego trójkąta

Artur z miasta Neptuna:

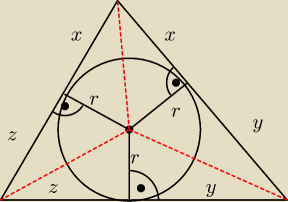
⎧	x+y = 4
⎨	y+z = 6
⎩	z+x = 8

z tego wyznaczysz x,y,z później masz trójkąty prostokątne i z tw. Pitagorasa obliczasz przeciwprostokątne (przerywane czerwone). Powyższy układ równań wynika z podobieństwa trójkątów i jest ściśle powiązany przy wpisywaniu okręgu w trójkąt.

Zygmuś: nieco przesadziłeś przyjacielu!To nie tak bezczelnie proste,jak tworkowo medialno−telewizyjna prostytutka.Gdzie masz r ?Dalszy wywód rzeczywiście poprawny ,ale gdzie masz r

Artur z miasta Neptuna: a co mnie 'r' obchodzi wiem tylko że 'r' wszędzie jest 'jednakowy' z podobieństwa wiem, że skoro mamy Δ prostokątny z (np.) przyprostokątną i przeciwprostokątną jednakowymi do przyprostokątnej i przeciwprostokątnej innego Δ to wiem, ze te dwa Δ są jednakowe.

Artur z miasta Neptuna: okey ... już wiem o co Ci chodziło.

Artur z miasta Neptuna: no nic ... to trzeba 'na chama'

	a+b+c
wzór Herona na pole Δ PΔ = √p(p−a)(p−b)(p−c) ; gdzie p =		=> PΔ = P{9*1*3*5}
	2

= 3√15

	2PΔ		6√15		√15
r =		=		=
	8+6+4		18		3

i już lecisz z tw. pitagorasa.

Basia: Zygmuś nie pozwalaj sobie. Jeszcze jeden taki wpis jak ten, który zaraz skasuję i nie tylko nikt Ci nie pomoże, ale zostaniesz zablokowany.