proszę o pomoc :( kasiaaa: 1.Udowodnij że schemat jest tautologią [(p∧∼s)⇒q{[(r∨s)⇒∼q]⇒(p⇒r)} 2.Oblicz całkę( x + ułamek jest do pierwiastka )

	cos2x
∫=(43√x5+		)dx
	sin2xcos2x

3.Zbadaj przebieg zmienności funkcji

	x2−16
y=
	x−3

4.Znajdź najmniejszą i największą wartość funkcji f(x,y)=2x²+y³−4x na kole opisanym nierównością : x²+y²≤36 5.Oblicz pole powierzchni ograniczonej wykresem funkcji f(x)=x²+5x+6 i osią OX z góry dziękuje

Man in black: Lepiej każde zadanie rozpisz jako osobny wątek.

kasiaaa: :(

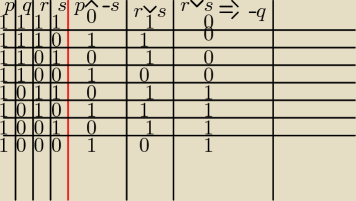
Artur z miasta Neptuna: [(p∧∼s)⇒q{[(r∨s)⇒∼q]⇒(p⇒r)} −−− a dla 'q' nie ma tutaj żadnego nic? tabelkę zacząłem robić, ale za dużo roboty z tym ... nie chce mi się zresztą ... nawet wszystkich przypadków nie zmieściłem (raptem połowę − bo tylko dla p = 1)

Man in black: Ad. f'_x=0 f'_y=0 ⇔ 4x − 4 =0, 3y²=0 ⇔ (x,y)=(1,0). Jedyny punkt wewnątrz koła w którym może być wartość ekstremalna, pozostałe na okręgu... Ale tu trochę więcej roboty. Teraz nie mam czasu − jak się nie pali to wieczorem będzie...

Man in black: Tautologie to chyba wykazałbym bez metody 0−1, ale muszę mieć dobrze nawiasu i funktory zapisane...

kasiaaa: [(p∧∼s)⇒q]⇒{[(r∨s)⇒∼q]⇒(p⇒∼r)} sorki to ma być tak

kasiaaa: ok może być i wieczorkiem o tych ekstremach

Man in black: Kiedy implikacja fałszywa: gdy następnik {[(r∨s)⇒∼q]⇒(p⇒∼r)} to 0 (a poprzednik [(p∧∼s)⇒q] to 1). Następnik 0, jedynie gdy [(r∨s)⇒∼q] = 1 i (p⇒∼r)=0. Czyli gdy p=1 i r=1, q=0. Rozważmy więc dwa przypadki: s=0 i s=1. s=0. Wtedy [(p∧∼s)⇒q] = 0 czyli cała implikacja jest prawdziwa. s=1 Wtedy [(p∧∼s)⇒q]=1 oraz {[(r∨s)⇒∼q]⇒(p⇒∼r)}=0. Czyli to nie jest tautologia! Sprawdź spokojnie sama dla: p=r=s=1, q=0.

kasiaaa: a tam będzie tylko 8 a nie więcej bo 8 to uczyłam się na trzech literach(p,q,r) no i nie wiem czy tu nie będzie tego więcej ?

Man in black: Jak 0−1 to 16 przypadków. Przeczytaj com napisał o 10:08, bom się namęczył trochę

kasiaaa: no teraz to ja juz sama nie wiem może ja to sama sprawdzę tylko ty mi wypisz jak mam to tabelkę zrobić − co gdzie wstawić bo zawsze coś gubię nie rysuj tylko napisz wyraz i oddziel go krechą

Man in black: Sprawdź tylko wartość logiczną całości dla tego przypadku: p=r=s=1, q=0. Wychodzi fałsz, bzdura, nieprawda, kłamstwo... Tabelkę złożoną z 16 wierszy możesz sobie wtedy odpuścić.

kasiaaa: nie mogę bo ona musi być jak tego nie zrobię to mi nie uzna

Man in black: Nie dziwię się więc, że tyle osób nie znosi matematyki... Sorry, ale w taki razie może pomoże Ci ktoś inny − dla mnie to bzdury, zapisywanie czegoś bez sensu i z góry skazanego na niepowodzenie tylko dlatego, aby kogoś zadowolić... Nie myślę o Tobie. Musisz kontynuować tak jak Artur zaczął...

kasiaaa: no wiem właśnie ja chcę tą metodą co ona ale hmmm.....ale nie wiem jak mam się do tego zabrać

Man in black: Ad 5. Pole = ∫₋₃⁻²−(x²+5x+6)dx ∫−(x²+5x+6)dx = − (x³/3 +5/2 *x² +6x) +c = F(x) Twoje pole to F(−2) − F(−3) − zrób wykres tej paraboli − −2 i −3 to jej zera.

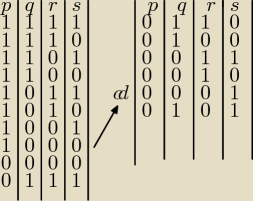
kasiaaa: dobrze to zrobiłam ?

Man in black: Jeżeli się nie powtarzają to dobrze

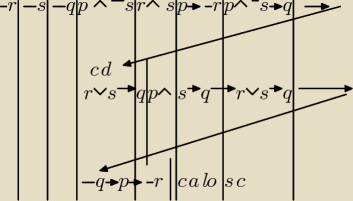
kasiaaa: raczej nie a tam dalej jak to rozpisać tak będzie dobrze czy czegoś nie zjadłam lub czy nie dałam za dużo ? ( − kreski to negacja)

kasiaaa: hej sprawdzi ktoś czy to będzie dobrze , czy czegoś nie zapomniałam wstawić?

kasiaaa: hej sprawdzi mi to ktoś lub napisze jak powinno być tą drugą metodą zakładającą że to np. jest nie prawda ?