Paulina: Proszę o pomoc− sprawdzenie wyniku. W trójkąt prostokątny o przyprostokątnych długości 2/3 i 2 wpisano okrąg. Oblicz odległość środka okręgu od wierzchołka kąta prostego tego trójkąta. r =0,5 AS=¹₂√2≈0,7

Zygmuś:

	ab
r=?=
	a+b+√a2+b2

d=?=√r²+d₁² ; d₁=¹₄(a+b−3√a²+b²) a,b (²₃ i 2)

Aga1: x=? c²=a²+b²

	2
a=
	3

b=2

	4		2√10
c=√		+4=
	9		3

	a+b−c
r=
	2

d=b−r x²=r²+d²

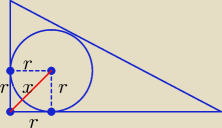
Bogdan: "Oblicz odległość środka okręgu od wierzchołka kąta prostego tego trójkąta." a, b − przyprostokątne, c − przeciwprostokątna.

	2		2
a =		, b = 2, c = √(4/9) + 4 =		√10
	3		3

	1		1		2		2		4		1
r =		(a + b − c) =		(		+ 2 −		√10) =		−		√10
	2		2		3		3		3		3

x = r√2

Paulina: Właśnie ja też tak zrobiłam i znalazłam swój błąd, ponieważ podstawiłam √3{2} a nie √2{3}. Dziękuję Bogdan!

Paulina: * ³₂ a nie ²₃