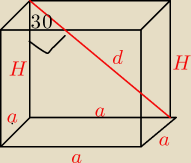
graniastosłupy Marcin: pole powierzchni bocznej graniastosłupa prawidłowego czworokątnego ynosi 48√3. przekątna ściany bocznej graniastosłupa tworzy z krawędzią boczną kąt 30 stopni. oblicz długość tej przekątnej

krystek: P_b=4a*H 4a*H=48√3

H
	=ctg30 i licz
a

Marcin: można prosić o pomoc dalej bo coś mi nie idzie

krystek: Licz ,poprawię!

Marcin: nie wiem co mam zrobić z równaniem 4a*H=48√3 jakaś mała wskazówka?

krystek: wyznacz H lub a i podstaw do drugiego Musisz na końcu policzyć d

krystek:

	12√3
H=
	a

Marcin: doszedłem do równania 48√3=4a*a√3

ejendi: Pb=4ah=48√3

	√3
cos30=
	2

sin30=1/2 tg30=√3/3 h=pcos30 a=psin30 a=48√3/h a=htg30 h²=12√3/tg30 p²=48

krystek:

12√3
	=√3
a2

a²=12 a=2√3 I teraz

a
	=sin30
d

2√3		1
	=
d		2

d=..

Marcin: naprawdę Ci dziękuje jestem wdzięczny z tym że niestety nic nie łapie z tego można jakoś prościej?

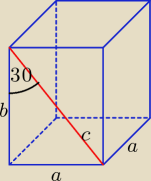
Bogdan: a > 0 i b > 0.

	a
4ab = 48√3 i		= tg30o
	b

	a		√3		√3
ab = 12√3 i		=		⇒ a =		*b
	b		3		3

√3		√3
	*b*b = 12√3 /*√3 ⇒ b2 = 36 ⇒ b = 6 i a =		*6 = 2√3
3		3

Z twierdzenia Pitagorasa c = √a² + b² = ...