zw
tomaszewski: mam pytanie,
f(x)=|−x+y|
można z tego wyznaczyć zbiór wartości?
20 lut 22:56
Man in black: Tak: f(x)≥0, jeżeli np. x∊R
20 lut 22:57
Man in black: zakładam, ze y nie zależy od x...
20 lut 22:58
Artur z miasta Neptuna:
y = |−x+y|
1. y≥x
y = −x + y ⇔ x=0 ⋀ y∊R
czyli: f(x) = 0
2. y<x
| | x | |
y = x − y ⇔ 2y = x ⇔ y = |
| −−− spełnione dla x>0 |
| | 2 | |
ostatecznie:
| | ⎧ | 0 dla x = 0 | |
| f(x) = | ⎩ | x/2 dla x>0 |
|
Uwaga
D
f = <0;+
∞), wynika to z tego, że f(x) > 0, więc x nie może być mniejszy od 0.
20 lut 23:01
Artur z miasta Neptuna:
oczywiście do 1.
x= 0 ⋀ y ≥ 0
20 lut 23:02
Man in black: tomaszewski: studia czy szkoła? Nie widzę powodu, aby y=f(x)...
20 lut 23:30
Man in black: Najsensowniej zapisałbym to tak f(x,y)=|x−y| i teraz zapytałbym o wartości.
Matematyka wymaga precyzji...
20 lut 23:36
Artur z miasta Neptuna:
nie no ... f(x) = |−x+y| ... i albo jest to funkcja uwikłana czyli y∼f(x) ... albo jest to
funkcja jednej zmiennej i 'y' jest parametrem (tyle że wtedy wchodzimy w 3D)
20 lut 23:59
Man in black: Jasne, ale utożsamianie y z f(x) jest kompletnie bezzasadne. My, na Marsie funkcje oznaczamy
tak np. (liniowa):
Ó(ź)= 2ź − 6.
I skąd mam wiedzieć, że y to Ó(x) ?
21 lut 00:03
Man in black: Jeszcze jedno: skoro to ma być funkcja uwikłana f(x) = |x−y| to należy podać czym jest f... Np.
f(x) = sinx. I wtedy mamy piękną funkcję uwikłaną...
21 lut 00:05
Artur z miasta Neptuna:
niby tak ... z drugiej jednak strony, jeżeli jest to funkcja jednej zmiennej, a 'y' jest
parametrem to dostajemy wtedy połowę R3
21 lut 00:06
Man in black: Połowę R3? Jeżeli y jest parametrem to zbiór wartości to f(x)≥0.
21 lut 00:09
Artur z miasta Neptuna:
ale ów parametr nie jest w żaden sposób ustalony więc y∊R, x∊R i f (czy tam z) ∊R
+ ... no i
mamy połowę R
3 zmasakrowaną przez tą funkcję
21 lut 00:11
Man in black: Zbiór wartości dotyczy zapewne funkcji f, a ona ma wartości w R
Dobra, odpuśćmy...
21 lut 00:14
Bogdan:
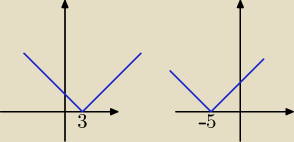
A może tak należy rozumieć to zadanie:
f(x) = |−x + y| ⇒ f(x) = |x − y|, y jest tu parametrem,
np. dla y = 3: f(x) = |x − 3|, dla y = −5: f(x) = |x + 5|.
Dla dowolnej wartości y∊R zbiorem wartości funkcji f(x) jest zbiór liczb rzeczywistych
nieujemnych.
21 lut 00:16
Artur z miasta Neptuna:
mi nie chodziło o zbiór wartości w tym momencie ... ale właśnie −−− odpuśćmy
21 lut 00:16
Man in black: Parametr, czy y=f(x) − w sumie mało ważne. Odpowiedź taka sama
21 lut 00:17