Geometria analityczna równanie okręgu
opornyyy: Hejka mam małą prośbę o wytłumaczenie mi pewnej kwestii.
Mam dane równanie okręgu x
2+y
2−4x+2y−20=0 i mam narysować ten okrąg.
W jaki sposób się do tego zabrać. Jak wyznaczyć środek tego okręgu. Proszę o pomoc

Z Góry dziękuję.
19 lut 21:19
Hurwitz : (x−2)2 + (y+1)2 = 52.
Porównaj z równaniem okręgu i masz środek i promień.
A jak się zabrać za rysowanie: ołówek w dłoń i do dzieła.
To było ostatnie zadanie na dziś...
19 lut 21:22
joł jołaj: co wiesz czego nie wiesz?
19 lut 21:24
Aga1: Różnie, ale można skorzystać ze wzoru ogólnego okręgu
x2+y2−2ax−2ay+c=0, gdzie c=a2+b2−r2,
czyli r=√a2+b2−c
Tu środek okręgu S=(a,b), r− promień okręgu
−2a=−4, −2b=2, c=−20
stąd
S=(2,−1)
r=√4+1+20=5
19 lut 21:26
joł jołaj: Zaraz Ci rozpiszę jak mi to nauczycielka tłumaczyła, szybko zrozumiałem

19 lut 21:28
opornyyy: Aha czyli to x
2+y
2−2ax−2by+c=0 to jest postać ogólna okręgu. Wystarczy że za
a i
b
podstawie moje dane czyli −4 i 2.
−2a=−4
−2b=2
Rozwiązuje i to jest mój środek okręgu. A jeśli bym miał zamiast −4x −−−−−> −6x to tak samo
podstawiam...
−2a=−6


Mniej więcej to tak zrozumiałem

19 lut 21:40
joł jołaj: x2 + y2 −4x + 2y − 20 = 0
x2 + y2 −4x + 2y = 20
1 − uporządkuj
(x2 −4x)(y2 + 2y) = 20
2 − zapoznaj się ze wzorem: (a − b)2
zajmijmy się 1 przypadkiem:
(x2 −4x) < −−−− żeby stworzyć wzór skróconego mnożenia brakuje liczby − wartość 4x dzielisz
przez 2x i do kwadratu = 4. Teraz taki myk, ze dodajesz 4 i odejmujesz 4. Czyli nie robisz
błędu, bo równie dobrze można zapisać postać (x2 −4 + 0 + 0 − 0 itd...itd..)
więc:
(x2 − 4x +4 − 4)
tutaj wzór (a + b)2
drugi przypadek:
(y2 + 2y) < −− to samo, dzielisz na 2x i do kwadratu (2y przez 2y = 1, a jeden do kwatratu to
też 1)
(y2 + 2y + 1 − 1)
teraz masz postać:
(x2 − 4x +4 − 4)(y2 + 2y + 1 − 1) = 20
teraz przenosisz wartości −4 i −1 na drugą stronę (nie zapomnij o zmianie znaku)
(x2 − 4x +4)(y + 2y +1) = 20 +4 + 1
(x2 − 4x +4)(y + 2y +1) = 25
zauważ, że teraz oba nawiasy możesz sprowadzić do postaci wzoru skróconego mnożenia
(a − b)2 oraz (a + b)2
(x2 −2)(y2 + 1) = 25
Równanie okregu:
(x − a)2(x − b)2 = r2
a = ..........
b = ..........
r2 = ....... => r = ......
19 lut 21:42
Aga1: Bardzo dobrze zrozumiałeś., tylko oblicz a, b i r.
19 lut 21:43
pigor: ale najlepiej to...

tak :
x2+y2−4x+2y−20=0 ⇔ x
2−4x+4+y
2+2y+1−20=4+1 ⇔ (x−2)
2+(y+1)
2=25 ,
stąd
S=(2,−1) − środek okręgu , a
r=5 jego promień . ...

19 lut 21:44
Aga1: joł między nawiasami jest + i nie można go opuścić.
19 lut 21:45
Hurwitz : Rozprawa na temat tego, jak zmasakrować proste zadanie...
19 lut 21:46
joł jołaj:
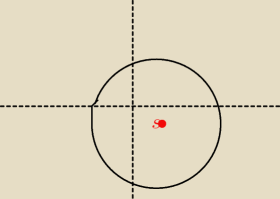
19 lut 21:47
joł jołaj: Aga1, jak nie można jak można, ja takim sposobem licze kazde zadanie
Hurwitz, jest cos w tym nie zrozumialego? Matematyki człowiek nie uczy sie na pamiec...
19 lut 21:49
opornyyy: Dzięki wielkie za wszystkie podpowiedzi. Ja sobie to przeanalizuje i myślę że zrozumiem.
Jeszcze raz dzięki wielkie

19 lut 21:50
Hurwitz : Aga1 − szanuję Cię, bo widziałem kilka Twoich dzieł, ale uwierz mi, to nie jest matematyka...
19 lut 21:52
Aga1: ale to co zapisałeś nie jest równaniem okręgu.
x+y≠xy.
19 lut 21:52
Aga1: Od czegoś trzeba zacząć.
19 lut 21:53
joł jołaj: zauważyłem, może i mój błąd:
(x −2)(y2 + 1) = 25
powinno byc tak:
(x −2)2(y + 1)2 = 25
Teraz możemy spekulować
19 lut 21:54
Aga1: Jeszcze jest żle.
Powinno być tak
(x−2)2+(y+1)2=25
19 lut 21:56
joł jołaj: ja nie widzę błędu i nauczycielka z matematyki też nie...
19 lut 22:00
krystek: @joł popatrz dobrze na zapis Agi
19 lut 22:02
krystek: I porównaj ze swoim MA być SUMA


19 lut 22:03
joł jołaj: tak, zapomniałem o tym plusie...
To nie jest usprawiedliwienie, ale rozpisywanie zadania na tym edytorze a w zeszycie to tutaj
jednak można się łatwiej pomylić...sorry moj blad.
19 lut 22:08
joł jołaj: ale jezeli chodzi o schemat rozpisywania to ja nie widze zadnego błędu, a ktoś wyzej mial
pretensje.
19 lut 22:09
 Z Góry dziękuję.
Z Góry dziękuję.


 Mniej więcej to tak zrozumiałem
Mniej więcej to tak zrozumiałem 
 tak :
x2+y2−4x+2y−20=0 ⇔ x2−4x+4+y2+2y+1−20=4+1 ⇔ (x−2)2+(y+1)2=25 ,
stąd S=(2,−1) − środek okręgu , a r=5 jego promień . ...
tak :
x2+y2−4x+2y−20=0 ⇔ x2−4x+4+y2+2y+1−20=4+1 ⇔ (x−2)2+(y+1)2=25 ,
stąd S=(2,−1) − środek okręgu , a r=5 jego promień . ...



