Wykaż, że jeżeli w trójkącie ABC Daroili93: Wykaż, że jeżeli w trójkącie ABC : |BC|² = |AC|² + |AC|*|AB| to jeden z kątów trójkąta jest 2 razy większy od drugiego.

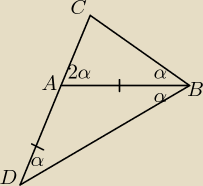
Vax: Odłóżmy na prostej CA taki punkt D (leżący bliżej punktu A), że |AD| = |AB|, wtedy założenie przyjmuje postać:

	|BC|		|CD|
|BC|2 = |AC|(|AC|+|AB|) = |AC|*|CD| ⇔		=		a to nam daje, że ΔABC ~
	|AC|		|BC|

ΔDBC czyli <BDA = <CBA = α, ale trójkąt DBA jest równoramienny więc też α = <ABD czyli <BAC = 2α cnd.