ostrosłup matroz: każda z krawędzi bocznych ostrosłupa tworzy z płaszczyzną podstawy kąt α. Podstawą tego ostrosłupa jest trójkąt prostokątny o przeciwprostokątnej 2c i kącie ostrym γ. oblicz objętość ostrosłupa.

Piotruś Pan: Gdzie leży w takim ostrosłupie spodek wysokości? Odpowiedź na to pytanie jest kluczem do rozwiązania zadania.

matroz: na środku przeciwprostkkątnej podstawy. To wiem ze wskazówki zawartej w książce, ale nie rozumiem dokladnie dlaczego, mógłbyś wyjaśnić?

	2
wynik to:		c3sinγcosγtgα
	3

moje rozwiązanie: http://www.fotosik.pl/pokaz_obrazek/784cfa7bc5e5f5c9.html jak widac, mój wynik jest inny, ale − i tu moje pytanie − czy może też być prawidłowy?

matroz: odświeżam, proszę o sprawdzenie

matroz: ?

Mila: Moim zdaniem , źle, bo założyłeś, że trójkąt ABC jest równoramienny. tgα=H/c H = c*tgα −wysokość ostrosłupa. Poczekaj , policzę i zrobię wtedy rysunek.

matroz: okpoczekam

Mila: tgα=H/c w ΔCDS H=c*tgα

	a		b
W ΔACB: sinγ=		oraz cosγ=
	2c		2c

a=2c*sinγ b=2c*cosγ dokończ

Piotruś Pan:

a
	= sinγ ⇒ a = 2csinγ
2c

b
	= cosγ ⇒ b = 2ccosγ
2c

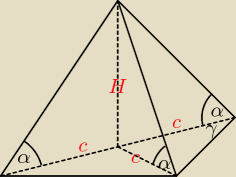
	1		1
Pole podstawy ostrosłupa PP =		ab =		*2csinγ*2ccosγ = c2sinγcosγ = c2sin2γ
	2		2

H
	= tgα ⇒ H = c*tgα
c

	1		1
Objętość V =		*c2sin2γ*c*tgα =		*c3sin2γ*tgα
	3		3

Przypominam, że sin2γ = 2sinγcosγ

Piotruś Pan:

Aga1: Jeśli każda krawędź ostrosłupa tworzy z płaszczyzną podstawy kąt α, to spodek wysokości ostrosłupa pokrywa się ze środkiem okręgu opisanego na podstawie

Mila: Brawo AGA!. Mało kto o tym pamięta.

Piotruś Pan: A co ja pokazałem? właśnie tę zależność.

Mila: Piotruś Twój rysunek jest wspaniały, komentarz Ciebie nie dotyczył, to ja mam do czynienia z różnymi uczniami i nie pamietają o tym.

Aga1: Nie gniewaj się Piotrusiu Godziu jak Ty rysowałeś, to ja pisałam.

Piotruś Pan:

Mila: A Matroz śpi?