Równanie symetralnej&środek i promień okręgu wojtek;): Witam. Mam wątpliwości co do dwóch zadań pierwsze: Znajdź równanie symetralnej odcinka AB : A=(5,−1) B=(−3,3) S=(x,y) A=(5,−1) ; B=(−3,3) x=1 ; y=1 S=(1,1) y=ax + b −1 = 5a + b / *(−1) 3= −3a + b 1 = −5a − b 3= −3a + b 4 = − 8a /−8) a=−1/2 y=ax + b 1=1*(−1/2) + b 1= −1/2 + b b= 1 1/2 (1,5) y= −1/2 x + 1 1/2 (1,5) Dobrze to jest? A jeśli źle to jakie powinno być rozwiązanie. I drugie zadanie Podaj środek i promień okręgu o równaniu a) (x−5)² + (y−3)² = 36 Prosze o dokładne rozpiasnie co i jak

krystek: II (x−a)²+(y−b)²=r² gdzie (a, b)⇒ współrzędne środka, r promień

krystek: pierwsze prawidłowy tok ( same rachunki nie sprawdzane)

wmboczek: do momentu a i b dobrze masz znaleźć symetralną, czyli −1/2*A=−1 prosta y=Ax+B przez pkt (1;1) środek (5,3) − liczby odejmowane w nawiasach, promień √36=6

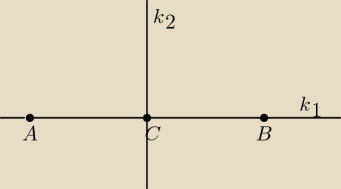
Piotruś Pan: Krystek − "pierwsze prawidłowy tok". A nieprawda. Tok do dupy. Na proces rozumowania, czyli poprawny tok składa się wiele czynników, nie tylko otrzymanie prawidłowego wyniku, ale także droga do tego wyniku. Im bardziej pokręcona, tym gorzej.

	5 − 3		−1 + 3
A=(5,−1), B=(−3,3), C = (		,		) = (1, 1)
	2		2

	3 + 1		4		−1
k1: y = a1x + b1, a1 =		=		=		,
	−3 − 5		−8		2

k₂: y = a₂x + b₂, k₂⊥k₁ ⇒ a₂ = 2, C∊k₂, y = 2(x − 1) + 1 ⇒ y = 2x − 1 i tyle.

pigor: ... lub z równania prostej przez 2 punkty :

	x+3		y−3
AB :		=		⇔ x+2y−3=0 , więc 2x−y+C=0 − szukana prosta i jej
	5+3		−1−3

	5−3		−1+2
punkt (x,y)=(		=1,		=1) , czyli 2−1+C=0 ⇒ C=−1 i 2x−y−1=0−
	2		2

− szukane równanie symetralnej danego odcinka AB . ...

Aga1: lub z własności punktu należącego do symetralnej. P(x,y)∊sym. AB⇔IAPI=IBPI IAPI²=IBPI² (x−5)²+(y+1)²=(x+3)²+(y−3)² x²−10x+25+y²+2y+1=x²+6x+9+y²−6y+9 −16x+8y+8=0 //:−8 odp.2x−y−1=0