prawdopodobieństwo. tomq: Rozwiąż zadanie : W urnie jest 8 kul czerwonych i jakaś liczba kul białych. Ile jest wszystkich kul w urnie, jeśli prawdopodobieństwo wylosowania 2 kul tego samego koloru jest równe 17/33 metodą drzewka

Mila: ze zwracaniem czy bez?

rumpek: 8 − liczba kul czerwonych n − liczba kul białych

	n + 8 2		(n + 8)!		(n + 7)(n + 8)
|Ω| = Cn + 82 =		=		=
			2*(n + 6)!		2

	n 2		8 2
|A| = C82 + Cn2 =		+		= ...

	17
P(A) =
	33

Drzewka są DO BANI

Mila: Drzewka są w niektórych sytuacjach bardzo dobre, tu lepiej tak, jak napisał Rumpek. Jeśli bedziesz się upierał, to narysuję. Ułóż równanie:

1   1   * n *(n−1) + *8 *7 2   2		17
	=
1   *(n+8)*(n+7) 2		33

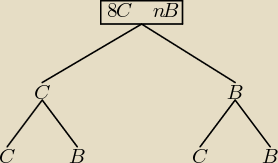
Piotruś Pan: Jeśli polecenie brzmi − metoda drzewka, to znaczy trzeba rozwiązać tą metoda i już. A− wylosowano kule rożnych kolorów.

	17		8		n − 1		n		8
P(A) =		i P(A) =		*		+		*
	33		n + 8		n + 7		n + 8		n + 7

	8		n − 1		n		8		17
Stąd		*		+		*		=
	n + 8		n + 7		n + 8		n + 7		33

Mila: Drzewko piękne, ale miały być kule tego samego koloru. Pasuje moje równanie.Z drzewka wychodzi bez 1/2.

Piotruś Pan: Chciałem, żeby tomq na wzór rozwiązania, które przedstawiłem sam doszedł do swojego rozwiązania

Mila: To przepraszam Cię Piotrusiu. Myślałam, że to nieuwaga.

Piotruś Pan: