oblicz sinus kąta wiktoria: Dolną podstawą sześcianu jest kwadrat ABCD. Punkt S jest punktem przecięcia przekątnych kwadratu A₁B₁C₁D₁ będącego górną podstawą sześcianu. Rozpatrzmy ostrosłup o podstawie ABCD i wierzchołku S. Oblicz sinus kąta, jaki z podstawą tego ostrosłupa tworzy: a) jego krawędź boczna b) wysokość jego ściany bocznej

Daria:

Daria:

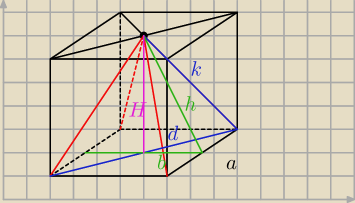
SAIzou: H = a (bo jest to zarówno wysokość ostrosłupa jak i sześcianu) d − połowa przekątnej kwadratu o boku a Z tw. Pitagorasa H² + d² = k²

	a√2
a2 + (		)2 = k2
	2

	3		√6
k2 =		a2 → k =		a
	2		2

	H		a		2		√6
sinα =		=		=		=
	k		√6   a 2		√6		3

============================================== b − połowa boku kwadratu H² + b² = h²

	1
a2 +		a2 = h2
	4

	5		√5
h2 =		a2 →h =		a
	4		2

	H		a		2√5
sinβ =		=		=
	h		√5   a 2		5