help Ania: Jeden z kątów trójkąta o obwodzie 6 ma miarę 60^o, a stosunek długości boków zawartych w ramionach tego kąta jest równy 1:2. Oblicz pole trójkąta.

joł jołaj: też jestem ciekawy

A ku ku:

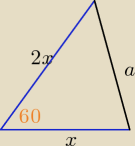
	1		x2*√3
P=		*2x*x*sin60o =
	2		2

oraz 2x+x+a=6 ⇒ a+3x= 6 ze wzoru cosinusów wyznacz a a²= x²+4x²−4x²*cos60^o a²= 3x² ⇒ a=x√3 to: a+3x=6 ⇒ x√3+3x= 6 ⇒ x=......... P=........... dokończ ........

Ania: ok, dzięki a takie zad: suma długości boków AC i AB trójkąta o polu 40√3 jest równa 26. Kąt BAC ma miarę 60^o.Oblicz odległośćod boku BCpunktu, który jest jednakowo odległyod wszystkich wierzchołków tego trójkąta.

A ku ku: P= 6(√3−1) [j²]

A ku ku:

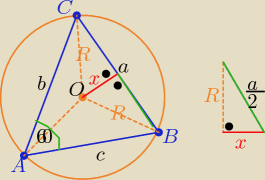
	1
P=		b*c*sin60o ⇒bc√3= 40√3
	2

to b*c= 160 i ⇒ b= 10 c= 16 lub b= 16 c= 10 b+c= 26 Punkt O jest środkiem okręgu opisanego na tym trójkącie ze wzoru cosinusów wyznacz długość boku "a" i ΔBOC jest równoramienny o ramionach R

	a
ze wzoru sinusów		= 2R ⇒ R= ....
	sin60o

teraz wyznacz długość x ...........

Bobi: Aj głowiłem się już pod koniec z wyznaczeniem X. w błąd mnie wprowadzi ten rysunek, wydaje mi się że powinien wyglądać tak