trgonometria rownanie Tomek: Zbadaj dla jakich wartości parametru m istnieją rozwiązania równania: √3sinx + cosx = m

Święty:

	√3		1
2(		sinx+		cosx)=m
	2		2

	π
2sin(x+		)=m
	6

	π
Dalej narysować wykres funkcji y=2sin(x+		) i prosta sprawa
	6

Tomek: dzieki

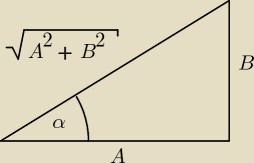Trivial: Najłatwiej 'zwinąć' pod jedną funkcję trygonometryczną. Algorytm jest bardzo prosty. W ogólności

	A		B
Asinx + Bcosx = √A2+B2(		sinx +		cosx).
	√A2+B2		√A2+B2

	A		B
Zauważmy teraz, że wyrażenia		oraz		tworzą parę cosinus−sinus
	√A2+B2		√A2+B2

(patrz rysunek) pewnego kąta α. Możemy zatem napisać Asinx + Bcosx = √A²+B²(cosαsinx + sinαcosx) = √A²+B²sin(x+α). Kąta α szukamy rozwiązując układ równań

	A
cosα =
	√A2+B2

	B
sinα =
	√A2+B2

Metoda ta przydaje się w różnego typu zadaniach, a nie przedstawiają jej zazwyczaj w liceum, więc dokładnie objaśniłem skąd się bierze. Do tego zadania...

	√3		1
√3sinx+cosx = 2(		sinx +		cosx)
	2		2

	π		π
= 2(cos		sinx + sin		cosx)
	6		6

	π
= 2sin(x+		) = m
	6

Zatem

	π		m
sin(x+		) =
	6		2

Skąd natychmiast uzyskujemy prostą nierówność do rozwiązania

	m
−1 ≤		≤ 1
	2

m ∊ [−2, 2].